Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 17
Considere a Figura e elabore um problema para ajudar outros estudantes a entender melhor a transformada de Laplace de uma forma de onda simples e não periódica.
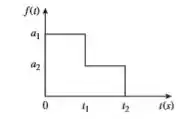
Passo 1
Poxa, existem muitas formas da qual você pode resolver esse problema, ou melhor, cria-lo (). Aqui nós vamos usar essa daqui:
PROBLEMA: Determine a função usando o conceito de função degrau. Em seguida, encontre a sua transformada de Laplace.
Passo 2
Bem, como a nossa função é antes de (nem aparece no desenho por ser irrelevante) e a função passa a ser no instante , podemos usar o conceito de função degrau para escrever isso:
Então, pelo menos até ...
SHOW! Quando chegamos em a função passa a ser (ela cai ), o que equivale a dizer em notação de degrau que...
Veja que antes de essa parcela é , já que , mas depois de ela vira então a função vira...
Que é o que a gente quer ! Mas atenção, ela não fica para sempre não! Observe na figura que em , esse degrau cai de para ():
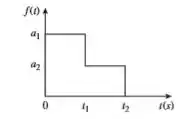
O que pode ser representado assim:
PRONTINHO! Agora a função segue para sempre, o que significas que acabamos a nossa missão de descrever a nossa função usando o conceito de função degrau !
Passo 3
Com isso pronto, agora podemos aplicar a transformada de Laplace:
Como e são constantes...
Ora, de acordo com a transformada de Laplace da função degrau...
Então...
E aí esta ela! A transformada de Laplace dos degraus da nossa figura !
Resposta
Ei, a resposta está no passo a passo :)