Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 42

Elabore um problema para ajudar outros estudantes a entenderem melhor como convoluir duas funções.

Passo 1

Vamos convoluir x ( t ) com y ( t ) dados nos gráficos abaixo

z t = x t * y ( t )

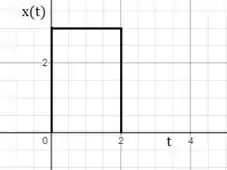
Nós vamos “deslizar” x ( t ) sobre o gráfico de y ( t ) e calcular a integral de convolução para vários intervalos, certo?

Primeiro vamos pegar o intervalo t < 2 :

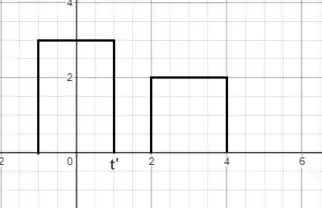
Nesse intervalo não há sobreposição dos gráficos, então, z t = 0 .

Passo 2

Para o intervalo 2 < t < 4 :

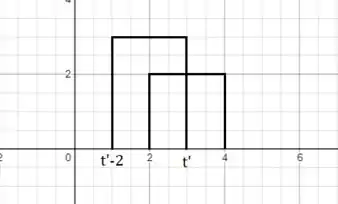
Nesse caso, há sobreposição dos gráficos de 2 até t ' , sendo que x t = 3 e y t = 2 , assim:

z t = ∫ 2 t ' 3.2   d t '

z t = 6 t - 12

Lembrando: estamos usando t ' como referência porque t já representa o nosso eixo das abscissas. Mas no resultado final podemos trocar t ' por t .

Passo 3

Para o intervalo 4 < t < 6 :

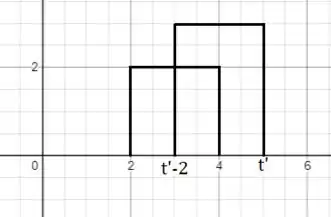
Agora, há sobreposição dos gráficos em t ' - 2 < t < 4

z t = ∫ t ' - 2 4 3.2   d t '

z t = 36 - 6 t

Passo 4

Por fim, para t > 6 :

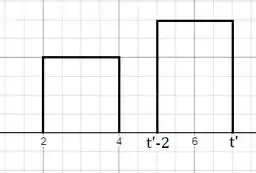
Nesse intervalo, não há sobreposição dos gráficos, portanto, z t = 0

E é isso aí, fizemos a integral de convolução para todos os intervalos possíveis, obtendo:

z t = 6 t - 12 ,   2 < t < 4 36 - 6 t ,   4 < t < 6 0 ,   c a s o   c o n t r á r i o

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro