Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 38
Consulte o circuito da Figura . Calcule para .
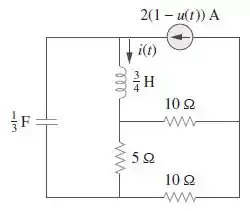
Passo 1
Vamos lá, galerinha! Da teoria de circuitos, sabemos que componentes como indutor e capacitor se comportam de maneiras diferentes dos resistores quando tem corrente circulando por eles. Para o capacitor, quando sob corrente por um longo tempo, o efeito causado no circuito é um circuito aberto; para o indutor, sob regime permanente, ele passa a funcionar como um curto-circuito. Assim, para o instante , o instante antes de , nós temos o seguinte circuito equivalente:
Vamos aplicar um divisor de corrente para encontrarmos o valor de .
Substituindo os valores,
A tensão pode ser calculada através da queda de tensão no resistor de . Assim,
Passo 2
Quando , a chave de abre e passamos a ter um circuito RLC série sem fontes! Mas de onde vem o resistor em série? Vamos fazer o equivalente!
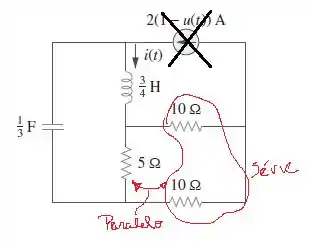
O equivalente dos resistores é:
Vamos agora encontrar as raízes características:
Como os valores de e são diferentes, temos a resposta natural com amortecimento supercrítico. As raízes são:
Desse modo, podemos escrever a corrente da seguinte forma:
Para , temos:
Além disso,
O que nos leva ao seguinte sistema de equações:
Resolvendo esse sistema, temos:
Logo,
Resposta
A corrente é igual a: