Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 52

A resposta a um degrau de um circuito R L C em paralelo é v = 10 + 20 e - 300 t cos ⁡ 400 t - 2 sen ⁡ 400 t   V ,   t ≥ 0 quando o indutor é de 50   m H . Determine R   e   C .

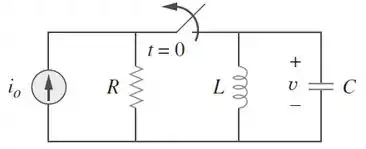
Passo 1

Pessoal, essa questão começa bem, até porque o enunciado já nos informa a expressão final para a tensão. Dela podemos retirar os valores de α e ω d ! Podemos escrever a expressão geral da tensão como:

v t = V S + A cos ⁡ ω d t e - α t + B sin ⁡ ω d t e - α t

Se reescrevermos nossa expressão original, teremos:

v = 10 + 20 cos ⁡ 400 t e - 300 t - 40 sen ⁡ 400 t e - 300 t   V ,   t ≥ 0

Assim, sabemos que α = 300 e ω d = 400 .

Passo 2

Vamos agora fazer o caminho inverso das expressões de α e ω d para encontrarmos os valores de R e C !

α = 1 2 R C = 30 0

ω d = ω 0 2 - α 2 = 400

ω 0 2 = ω d 2 + α 2 = 160000 + 90000 = 250000

Sabemos que ω 0 = 1 L C → ω 0 2 = 1 L C

1 L C = 250000

C = 1 250000 × 50 × 10 - 3 = 80   μ F

Agora que já sabemos o valor de C , podemos encontrar a resistência sem problemas:

R = 1 2 α C = 1 2 × 300 × 80 × 10 - 6 = 20,83   Ω

Resposta

Os valores de R e C são:

R = 20,83   Ω

C = 80   μ F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma tensão de ramo em um circuito R L C é descrita por d 2 v d t 2 + 4 d v d t + 8 v = 24 Se as condições iniciais forem v 0 = 0 = d v 0 d t , determine v t .
Um circuito R L C em série é descrito por L d 2 id t 2 + R d i d t + i C = 10 Determine a resposta quando L = 0,5H , R = 4Ω e C = 0,2F . Considere i 0 = 1 e d i 0 d t = 0 .
As respostas a um degrau de um circuito R L C em série são v C = 40 - 10 e - 2 t - 10 e - 4 tV , t0 i L t = 3 e - 2 t + 6 e - 4 tm A , t0 Determine CDetermine que tipo de amortecimento é apresentado p
Resolva as equações diferenciais a seguir sujeitas às condições iniciais especificadas d 2 v d t 2 + 4 v = 12 , v 0 = 0 ,d v 0 d t = 2 d 2 i d t 2 + 5 d i d t + 4 i = 8 , i 0 = - 1 ,d i 0 d t = 0 d 2
Obtenha v(t) e i(t) para t0 no circuito da Figura 8.84.