Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 42
Dado o circuito da Figura , determine para .
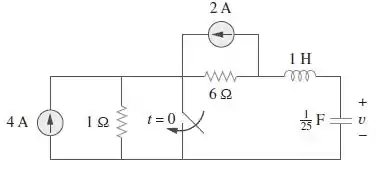
Passo 1
Vamos lá, galerinha! Quando estamos em , ou seja, no momento antes de , nós temos a chave aberta. Assim, o circuito fica com a seguinte cara:
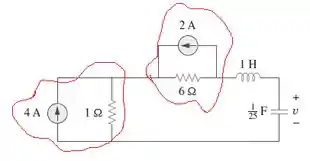
Podemos transformar essa fonte de corrente em paralelo com um resistor (circulado em vermelho) em uma fonte de tensão em série com um resistor. Para encontrarmos o valor da nova fonte de tensão, basta multiplicarmos a corrente gerada pelo valor da resistência. Assim,
Dessa maneira, podemos encontrar o valor da tensão no instante inicial:
Passo 2
Quando , passamos a ter o seguinte circuito (já aproveitando a transformação feita no passo anterior):
Vamos agora procurar as raízes:
Como as raízes são imaginárias, podemos escrever a tensão como:
Passo 3
Quando olhamos para o instante , temos:
A corrente de um indutor pode ser escrita como:
No instante ,
Portanto, a tensão final será igual a:
Resposta
A tensão é igual a: