Determine no circuito com amplificador operacional da Figura 18.50.
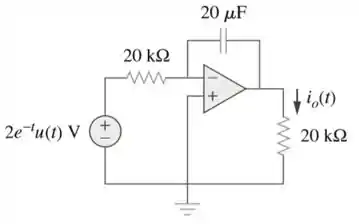
Passo 1
Nessas questões que envolvem Fourier e circuitos elétricos, a jogada da questão sempre vai estar na função de transferência do circuito. Por isso, é sempre importante que tenhamos atenção na hora de fazermos as questões, para não vacilar com o ! A primeira coisa a se fazer aqui, é transformar os componentes que estão no domínio do tempo para o domínio da frequência!
Passo 2
Estando no modo de integrador, temos que:
Para a corrente, teremos:
Portanto,