Use o método das transformadas de Fourier para obter no circuito da Figura 18.51.
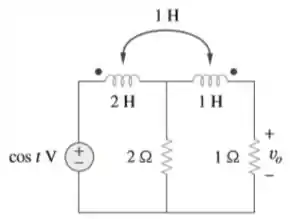
Passo 1
Nessas questões que envolvem Fourier e circuitos elétricos, a jogada da questão sempre vai estar na função de transferência do circuito. Por isso, é sempre importante que tenhamos atenção na hora de fazermos as questões, para não vacilar com o ! A primeira coisa a se fazer aqui, é transformar os componentes que estão no domínio do tempo para o domínio da frequência! Já transformando, vamos considerar o circuito abaixo:
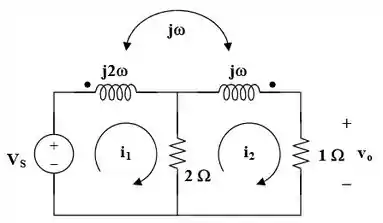
Passo 2
Primeiro, temos que a tensão é:
Isso por causa da simples transformação de .
Então, vamos continuar! Fazendo uma analise de malha, temos que para a malha 1:
Para a malha 2,
Passo 3
Agora misturando as malhas, jogando a malha 2 na malha 1, teremos:
Continuando,
Certo galera, agora o bixo pega! Vamos transformar isso para o domínio do tempo, pelo método da integral. Porque, acreditem, é o mais simples! Vamos lá!
Simplificando tudo isso, temos: