Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 14

Determine i ( t ) para t > 0 para o circuito na figura. Suponha i s t = 4 u t + 2 δ t   m A .

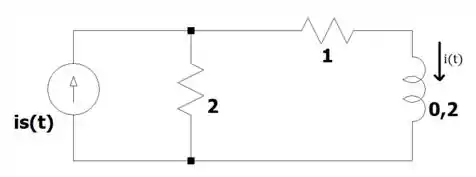
Passo 1

Vamos transformar nosso circuito pro domínio s beleza? Vamos ter isso aqui:

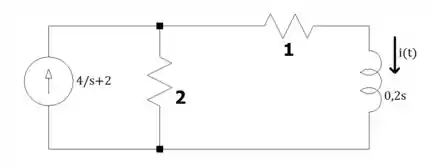
Hmm, lembra daquele teorema que podemos transformar uma fonte de corrente em paralelo com um resistor em uma fonte de tensão em série com esse resistor? Lembrando que V s = R . I ( s ) , a gente vai ficar com isso aqui:

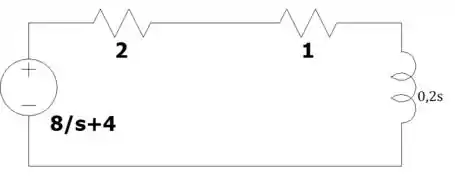
Passo 2

Agora que temos um circuito em série e a corrente é a mesma ao longo de todo o circuito, podemos escrever que:

I s = V s R

I s = 8 s + 4 2 + 1 + 0,2 s

I s = 8 s + 4 3 + 0,2 s

Multiplicando em cima e embaixo por 5 s (o 5 é só pra sumirmos com esse número decimal e o s pra tirarmos ele do denominador do 8 hahahah):

I s = 40 + 20 s 15 s + s ²

I s = 20 s + 40 s ( s + 15 )

Passo 3

Ufa, agora vamos fazer frações parciais para encontrarmos i ( t ) ? Bora lá!

20 s + 40 s ( s + 15 ) = A s + B s + 15

20 s + 40 = A s + 15 A + B s

20 s + 40 = s A + B + 15 A

Igualando os termos dos dois lados, temos:

A + B = 20 15 A = 40

Resolvendo esse sistema, a gente vai encontrar os valores de A e B :

A = 8 3

B = 52 3

Substituindo na expressão ali de cima:

20 s + 40 s ( s + 15 ) = 8 3 s + 52 3 s + 15

Fazendo a transformada inversa dessas duas fraçõezinhas:

i t = 8 3 + 52 3 e - 15 t u t   A

Resposta

i t = 8 3 + 52 3 e - 15 t u t   m A

Ver Outros Exercícios desse livro