Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 16
O capacitor no circuito da figura se encontra descarregado inicialmente. Determine para .
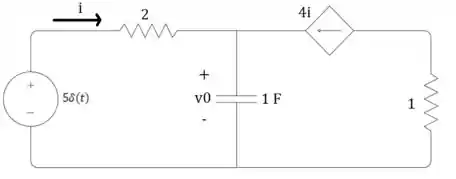
Passo 1
Vamos antes de tudo escrever nosso circuito no domínio , beleza? Então, lembrando que a transformada do impulso é e a transformada de é :
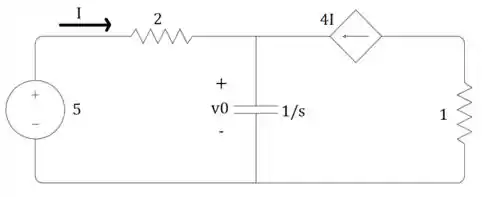
Passo 2
Do circuito, podemos analisar o nó acima do capacitor e colocar a corrente que passa por ele saindo desse nó. Assim, ficamos com a equação:
E fazendo as contas, isolando :
Mas, pelo circuito, podemos ver que:
Então:
Vamos isolar :
Fazendo a transformada inversa de :
Ou, se você preferir:
Beleza? Acabou!
Resposta
Exercícios de Livros Relacionados
Não há nenhuma energia armazenada no circuito da Figura P13.22, em t = 0-. a) Determine Vo. b) Determine vo. c) A solução para vo faz sentido em termos do comportamento conhecido do circuito? Explique
Não há nenhuma energia armazenada no circuito da Figura P13.19, em t = 0 - . a) Use o método das tensões de nó para determinar i 0 . b) Determine a expressão no domínio do tempo para v 0 . c) Suas res
Determine v o no circuito da Figura P13.23, se i g = 20u(t) mA. Não há nenhuma energia armazenada no circuito em t = 0.
A chave no circuito da Figura P13.11 esteve na posição x por um longo tempo. Em t = 0, ela passa instantaneamente para a posição y. a) Construa um circuito no domínio da frequência, para t0. b) Determ
A chave no circuito da Figura P13.15 esteve fechada por um longo tempo antes de abrir em t = 0. a) Construa o circuito no domínio da frequência, para t0. b) Determine I 0 . c) Determine i 0 tp a r at