Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 13

Considere a figura e elabore um problema para ajudar outros estudantes a entender melhor a análise de circuito usando as transformadas de Laplace.

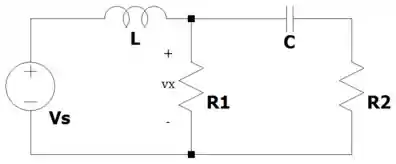
Passo 1

Aqui não tem resposta certa, então vamos selecionar apenas um dos problemas que você pode criar:

Encontre v x no circuito dado que V s = 2 u t   V , L = 1   H , C = 1   F , R 1 = 4   Ω e R 2 = 2   Ω .

O circuito com as impedâncias colocadinhas fica assim ó:

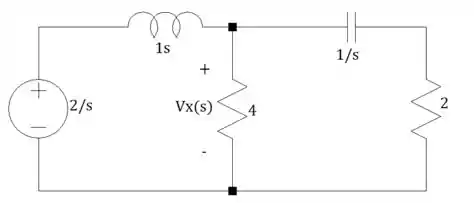
Passo 2

Pelo método de tensão dos nós, teremos:

V x ( s ) - 2 s s + V x ( s ) - 0 4 + V x ( s ) - 0 1 s + 2 = 0

Multiplicando em cima e embaixo por s :

s V x ( s ) - 2 s ² + s V x ( s ) 4 s + s V x ( s ) 2 s + 1 = 0

4 s + 8 s V x ( s ) - 2 + s V x s . 2 s 3 + s 2 + s V x s . 4 s ³ s 2 . 4 s . ( 2 s + 1 ) = 0

4 V x s - 8 s + 8 s V x s - 16 + 2 s 4 V x s + s ³ V x ( s ) + 4 s 4 V x ( s ) = 0

Colocando V x ( s ) em evidência:

V x s . 4 + 8 s + 2 s 4 + s 3 + 4 s 4 = 8 s + 16

V x s . 6 s 4 + s 3 + 8 s + 4 = 16 s + 8 s

Isolando V x ( s ) :

V x s = 16 s + 8 6 s 4 + s 3 + 8 s + 4 s

Resposta

V x s = 16 s + 8 6 s 4 + s 3 + 8 s + 4 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O amp op no circuito mostrado na Figura P13.47 é ideal. Não há nenhuma energia armazenada nos capacitores no instante em que o circuito é energizado. Determine (a) Vo, (b) vo e (c) quanto tempo o amp
Um pulso de tensão retangular, v i=[ u ( t )-u ( t-1 ) ]V , é aplicado ao circuito da Figura P13.59. Use a integral de convolução para determinar vo.
a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vi para o circuito na Figura P13.51.b) Determine o valor numérico de cada polo e zero de H(s).