Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 55

Determine as correntes de linha para o circuito trifásico da Figura 12.64. Seja Va = 110 0 , Vb = 110l 120 e Vc = 110 120 V.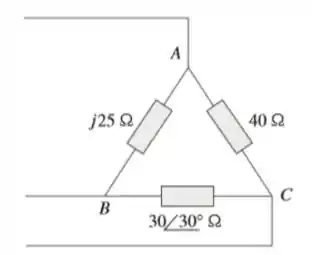

Passo 1

Vamos lá galera! A questão nos dá que a fonte é equilibrada, então quanto a isso é de boas! Quanto as tensões da fonte, a questão já nos dá a tensão de fase, para o fasor 0. Logo, para calcular a corrente de fase, basta pegar a tensão de fase (respectivamente defasadas) e dividir pelas impedâncias!

I A B = 240 j 25 = 9.6 ∠ - 90 ° A

I C A = 240 ∠ 120 ° 40 = 6 ∠ 120 ° A

I B C = 240 ∠ - 120 ° 30 ∠ 30 ° = 8 ∠ - 150 ° A

Passo 2

A potencia complexa em cada fase pode ser dada como:

S A B = I A B 2 Z A B = 9.6 2 j 25 = j 2304

S A C = I A C 2 Z A C = 6 2 40 = 1440

S B C = I B C 2 Z B C = 8 2 30 ∠ 30 ° = 1662.77 + j 960

Portanto, a potencia complexa total é a soma de todas, ou seja

S = 3102.77 + J 3264   V A

Resposta

I A B = 9.6 ∠ - 90 ° A

I C A = 6 ∠ 120 ° A

I B C = 8 ∠ - 150 ° A

S = 3102.77 + J 3264   V A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a Figura 12.63 e elabore um problema para ajudar outros estudantes a entender melhor os sistemas trifásicos não equilibrados.
Determine as correntes de linha para o circuito trifásico da Figura 12.64. Seja V a = 110 ∠0 °,V b = 110 ∠ -120°eV c = 110 ∠120 °V .
Resolva o Problema 12.10 usando o PSpice ou MultiSim.
Use o PSpice ou MultiSim para determinar Io no circuito monofásico trifilar da Figura 12.66. Seja Z 1 = 15-j 10Ω ,Z 2=30+j 20Ω eZ 3 = 12+j 5Ω .