Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 56
Considere a Figura 12.63 e elabore um problema para ajudar outros estudantes a entender melhor os sistemas trifásicos não equilibrados.
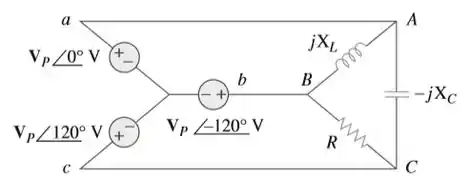
Passo 1
Vamos lá galera! Embora existam muitas maneiras de resolver esse problema, este é um exemplo baseado no mesmo tipo de problema solicitado na terceira edição. Então, o problema é o seguinte: Observando o circuito abaixo, determine as correntes de linha.
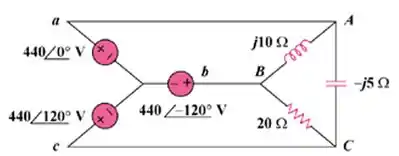
Passo 2
Para o item a), vamos definir as malhas dessa forma:
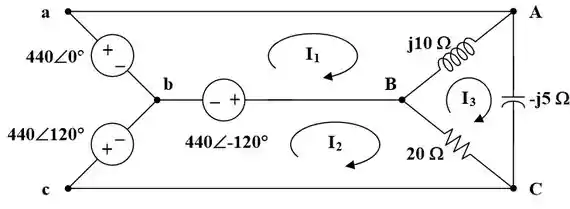
Para a malha 1,
Para a malha 2,
Para a malha 3,
Substituindo e simplificando a equação da malha 1 na malha 2, temos que:
Passo 3
Portanto da malha 1 e da malha 2, especificamente:
Agora fazendo uma LKC, temos que:
Resposta
Exercícios de Livros Relacionados
Use o PSpice ou MultiSim para determinar as correntes IaA e IaC no sistema trifásico desequilibrado mostrado na Figura 12.69. Seja Z l = 2 + j , Z 1 = 40 + j 20Ω Z 2 = 50 - j 30 Ω , Z 3 = 25Ω
Para o circuito da Figura 12.58, use o PSpice ou MultiSim para determinar as correntes de linha e as correntes de fase.
Um sistema trifásico quadrifilar operando com tensão de linha igual a 208V é mostrado na Figura 12.71. As tensões da fonte estão equilibradas. A potência absorvida pela carga resistiva conectada em es
Na Figura 12.73, dois wattímetros estão conectados apropriadamente à carga desequilibrada alimentada por uma fonte equilibrada tal que V a b = 208 ∠0 °V com sequência de fases positiva. a) Determine a
A Figura 12.76 mostra uma carga, que é um motor trifásico, em triângulo que é conectada a uma tensão de linha de 440 V e que absorve 4 kVA com fator de potência igual a 72% (atrasado). Além disso, um