Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 17

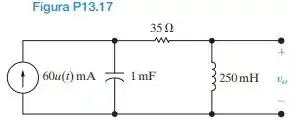
a) Determine a expressão de V o no domínio da frequência, para o circuito da Figura P13.17.

b) Use a expressão no domínio da frequência determinada em (a) para prever os valores inicial e final de v o .

c) Determine a expressão no domínio do tempo para v o .

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Inicialmente podemos definir V0 pela seguinte expressão:

    2. V 0 = I g C s 2 + R L s + 1 / L C

    Com isso, temos:

    I g C = 60 ;         R L = 140 ;         1 L C = 4000 ;

    E por fim:

    V 0 = 60 s 2 + 140 s + 4000

  2. Usando a expressão obtida no item anterior, temos que:

    3. s V 0 = 60 s s 2 + 140 s + 4000

    Logo:

    lim ⁡ s V 0 = 0 → v 0 ∞ = 0

    lim ⁡ s V 0 = 0 → v 0 0 + = 0

    Passo 2

  3. Para determinar o domínio de tempo, temos que:

V 0 = 60 ( s + 40 ) ( s + 100 ) = 1 s + 40 + - 1 s + 100

Por fim:

v 0 = e - 4 0 t - e - 100 t u t V

Resposta

  1. Item a:

    2. V 0 = 60 s 2 + 140 s + 4000

  2. Item b:

    3. lim ⁡ s V 0 = 0 → v 0 ∞ = 0

    lim ⁡ s V 0 = 0 → v 0 0 + = 0

  3. Item c:

v 0 = e - 40 t - e - 100 t u t V

Exercícios de Livros Relacionados

O amplificador operacional no circuito da Figura P13.54 é ideal. a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vg. b) Determine o valor numérico de cada zero e polo de H(s
O amp op no circuito mostrado na Figura P13.46 é ideal. Não há nenhuma energia armazenada nos capacitores no instante em que o circuito é energizado. a) Determine vo se vg1 = 40u(t) V e vg2 = 16u(t) V
O amp op no circuito mostrado na Figura P13.47 é ideal. Não há nenhuma energia armazenada nos capacitores no instante em que o circuito é energizado. Determine (a) Vo, (b) vo e (c) quanto tempo o amp