Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 37

a) Determine a corrente no resistor de 160 V no circuito da Figura P13.36. O sentido de referência para a corrente é de cima para baixo, passando pelo resistor.

b) Repita a parte (a), se o ponto no enrolamento de 250 mH for invertido.

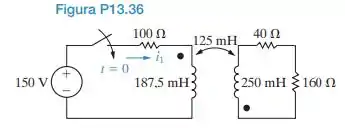
Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Da solução do problema anterior, temos que:

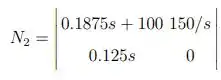
    2. Concluindo que N 2 = - 18,75 .

    Logo:

    I 2 = N 2 ∆ = - 600 s + 400 s + 1600

    Colocando em termos de K, temos que K 1 = - 0,5 ; K 2 = 0,5 .

    Concluindo:

    i 2 t = - 0,5 e - 40 t + 0,5 e - 1600 t u t A

    Passo 2

  2. Fazendo as mudanças necessárias, temos que:

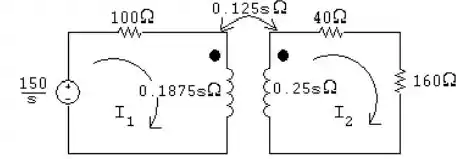
As duas equações ficam:

150 s = 100 + 0,1875 s I 1 - 0,125 s I 2

0 = - 0,125 s I 1 + 0,25 s + 200 I 2

Comparando essas equações com as do item acima, podemos concluir que:

i 2 t = 0,5 e - 400 t - 0,5 e - 1600 t u t A

Resposta

  1. Item a:

    2. i 2 t = - 0,5 e - 40 t + 0,5 e - 1600 t u t A

  2. Item b:

i 2 t = 0,5 e - 400 t - 0,5 e - 1600 t u t A

Exercícios de Livros Relacionados

Determine v_o ( t ) no circuito da figura.
Determine v ( t ) para t0 no circuito da figura.
Calcule as correntes de malha no circuito da figura. Apresente seus resultados no domínio s.
Determine i ( t ) para t0 no circuito da figura.
Para o circuito da figura, calcule i ( t ) para t0 .