Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 1
Determine a função de transferência do circuito na figura 14.68. Expresse-a usando
Passo 1
O Circuito dado no problema consiste de um capacitor em série com um resistor como mostrado abaixo
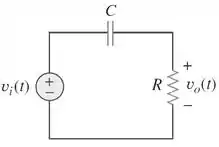
Passo 2
Cara! Seguinte! Pra dar prosseguimento e tu conseguir encontrar a função de transferência, vai ter que passar todos os componentes pro domínio da frequência.
Pra isso basta converter os componentes por suas respectivas impedâncias.
Como ?!
Assim Oh!
Pro Resistor sua impedância é igual a ele próprio, pois o mesmo não varia com a frequência.
Pro capacitor que varia sua impedância com a frequência teremos
O circuito equivalente será
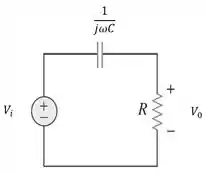
Passo 3
Mas e essa função de transferência ai?!
Bem a FT nada mais é que o comportamento do sistema definido como a razão entre a saída do sistema por sua entrada.
Aqui possuímos um circuito em série, logo a corrente é a mesma em cada elemento. Dessa forma a variável de saída é a tensão sobre o resistor e a variável de entrada é a própria tensão de entrada, sendo assim será:
Passo 4
A tensão é a tensão sobre o resistor e a tensão e a tensão de entrada é a soma da tensão no resistor mais a tensão no capacitor.
Multiplicando o lado direito da equação por , a FT ficará:
Passo 5
O problema nos deu a informação de que . Logo
Substituindo em
Resposta
A função de transferência é