Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 48

Determine a função de transferência V 0 / V s do circuito na Figura 14.86 . Demonstre que o circuito é um filtro passa-baixa.

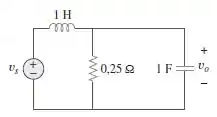
Passo 1

Galera, pelo divisor de tensão, só podemos achar a função de transferência H ( ω ) :

H ω = R | | 1 j ω C ( R | | 1 j ω C ) + j ω L

H ω = R j ω C R + 1 j ω C R j ω C R + 1 j ω C + j ω L

H ω = R j ω C R + 1 R j ω C R + 1 + j ω L

H ω = R R - ω 2 R L C + j ω L

Substituindo os valores,

H ω = 0,25 0,25 - 0,25 ω 2 + j ω

Passo 2

Se fizermos a frequência ω igual a 0 , temos:

ω = 0   →     H 0 = 0,25 0,25 - 0,25 ( 0 ) 2 + j ( 0 ) = 1

Agora, com ω = ∞ , temos:

ω = ∞   →     H ∞ = 0,25 0,25 - 0,25 ( ∞ ) 2 + j ( ∞ ) = 0

Como H 0 = 1 e H ∞ = 0 , temos a prova de que o circuito é um filtro passa-baixa.

Resposta

A função de transferência é:

H ω = 0,25 0,25 - 0,25 ω 2 + j ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O amplificador operacional no circuito da Figura P13.54 é ideal. a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vg. b) Determine o valor numérico de cada zero e polo de H(s
O amp op no circuito mostrado na Figura P13.46 é ideal. Não há nenhuma energia armazenada nos capacitores no instante em que o circuito é energizado. a) Determine vo se vg1 = 40u(t) V e vg2 = 16u(t) V