a) Determine a função de transferência Io/I g como uma função de , para o circuito da Figura P13.57.
b) Determine o maior valor de m que produzirá um sinal de saída limitado para um sinal de entrada limitado.
c) Determine para = -3, 0, 4, 5 e 6, se = 5u(t) A.

Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!
- Desenvolvendo o circuito acima, temos que:
- Dados os conhecimentos que adquirimos no item acima, temos que:
- Podemos demonstrar os dados pedidos através da tabela construída com cada cálculo:
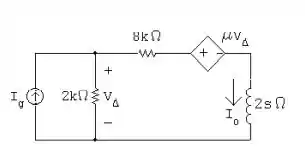
Disso, tiramos que:
Concluimos então que:
Passo 2

Todos os dados mostrados, podem ser obtidos através do seguinte passo a passo de cálculo:
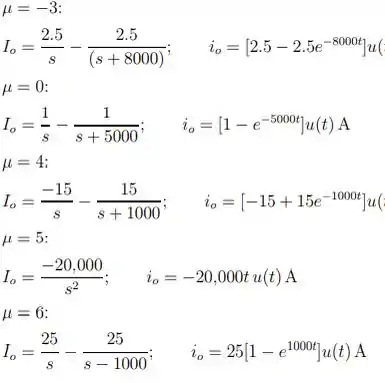
Resposta
- Item a:
- Item b:
- Item c:
