Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 54

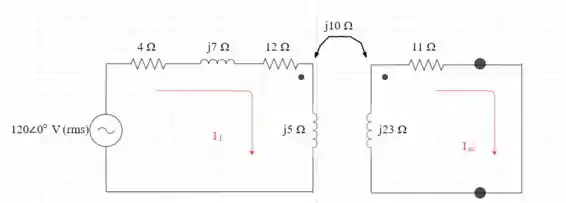
A impedância ZL no circuito da Figura P10.54 é ajustada para máxima transferência de potência média a ZL. A impedância interna da fonte de tensão senoidal é 4 + j7 V.

a) Qual é a máxima potência média fornecida a ZL?

b) Qual percentagem da potência média fornecida ao transformador linear é fornecida a ZL?

Passo 1

Beleza pessoal?! Estou vendo aqui e pelos meus cálculos você já pegou o lápis e o papel para acompanhar mais uma resolução de alto nível aqui no Responde Aí. Isso quer dizer que já posso começar né?!

  1. Primeiro iremos fazer algumas considerações. Desconectar a impedância de carga Z L

    2. para determinar a tensão de Thevenin V T h através dos terminais de carga, conforme mostrado na Figura

    O valor de V T h será então dado por

    V T h = 120 16   +   j 12 j 10

    = 36   +   j 48

    = 60 ∠ 53.13 º   V r m s

    conecte os terminais de carga através de um curto-circuito como mostrado, depois iremos escrever as duas equações das nossas duas malhas.

    A primeira malha é equacionada por

    120 = 16 + j 12 I 1 - j 10 I s c         ( 1 )

    A segunda malha é equacionada por

    0 = 11 + j 23 I s c - j 10 I 1

    I s c = 0.354 + j 0.169 I 1         ( 2 )

    Substituindo (2) em (1) para determinarmos I 1

    120 = 16 + j 12 I 1 - j 10 I s c

    = 16 + j 12 I 1 - j 10 0.354 + j 0.169 I 1

    I 1 = 5.52 - j 2.64

    = 6.12 ∠ - 25.56 º   A r m s

    Substituindo I 1 em (2) para podermos obter I s c

    I s c = 0.354 + j 0.169 5.52 - j 2.64

    = 2.4   -   j 0.00168

    = 2.4 ∠ - 0.04 º A r m s

    Agora determinando a impedância do equivalente de Thevenin

    Z T h = V T h I s c

    =   36   +   j 48 2.4   -   j 0.00168

    15 + j 20 Ω

    A potência média máxima é transferida para a impedância de carga Z L na condição de que

    Z L = Z T h *

    Z L = 15 - j 20 Ω

    Conecte o Z L calculado ao circuito equivalente de Thevenin como mostrado na figura

    Agora iremos determinar o valor da corrente

    I   =   V T h R T h + R L

      =   36   +   j 48 30

    =   1.2   +   j 1.6

    =   2 ∠ 53.13 º   A ( r m s )

    Agora iremos determinar a potência média dissipada

    P = I 2 R L

    = 2 2 15

    60   W

    Passo 2

  2. determine a impedância do lado secundário do transformador

Z 22 = Z L + 11 + j 23

= 15 - j 20 + 11 + j 23

= 26 + j 3 Ω

Agora determinar a corrente entregue pela fonte de voltagem I g

I g = Z 22 I j 10

=   26 + j 3 1.2 + j 1.6 j 10

=   4.52   - j 2.64

=   5.23 ∠ - 30.28 º   A ( r m s )

Determine a magnitude da potência média P g desenvolvida pela fonte de tensão,

P d = I g 2 12

= 5.23 2 12

=   328.23   W

Determinar a potência média P t entregue à transformação linear

P t = P g - P d

= 542.4   -   328.23

= 214.7   W

Agora finalmente chegamos a nossa última conta, vamos agora determinar a porcentagem da potência média entregue à carga

% e n t r e g u e = 60 214.17 100

=   28.02 %

Resposta

  1. P   =   60   W
  2. %   e n t r e g u e   =   28.02 %

Exercícios de Livros Relacionados

Calcule o valor eficaz da corrente em regime permanente através de resistor de 2 ⋅ Ω , se v r = 3 c o s ⁡ tV
Calcule o valor eficaz da corrente i em regime permanente e o fator de potência visto pelos terminais da fonte. Que elementos deve-se conectar em paralelo com a fonte para corrigir o fator de potência
Calcule o valor eficaz da corrente em regime permanente sobre o resistor de + Ω .
Calcule a potência media absorvida pelo capacitor, os dois resistores e a fonte.
Para um capacitor de C farads, conduzindo uma corrente i = I m c o s ⁡ ( ω t ) , verifique por (12.6) que a potência média é zero. Repita para um indutor de L henrys.