Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 30
- Determine a impedância de entrada do circuito da figura usando o conceito de impedância refletida
- Obtenha a impedância de entrada substituindo o transformador linear por seu circuito equivalente
Passo 1
Galerinha, vamos resovler a letra (a)! A intepedância de entrada pode ser escrita como:
Onde é a impedância do secundário refletida no primário do transformador. Vamos calcular ela primeiro:
Voltando a equação da impedância de entrada,
Passo 2
Agora, na letra (b) precisamos substituir o transformador linear por seu circuito equivalente com os seguintes parâmetros:
Assim, o circuito fica da seguinte forma:
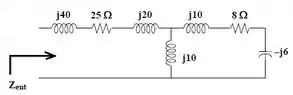
Assim, a impedância de entrada é igual a:
Resposta
Exercícios de Livros Relacionados
Para o circuito da Figura 13.127, determine: A potência complexa fornecida pela fonteA potência média liberada para o resistor de 18Ω .
Determine as correntes de malha do circuito da Figura 13.128.
Para o circuito da Figura 13.129, determine a relação de espiras de modo que a potência máxima seja liberada para o resistor de 30k Ω .
Calcule a potência média dissipada pelo resistor de 20Ω na Figura 13.130.
Determine a impedância de entrada do circuito com transformador de núcleo de ar da Figura 13.102 .