Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 6

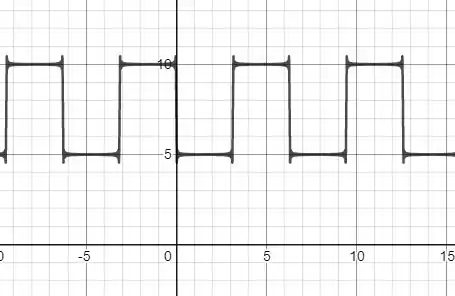
6- Determine a série de Fourier trigonométrica para

f t = { 5 ,   0 < t < π 10 ,       π < t < 2 π   e f t + 2 π = f ( t )

Passo 1

Bem com o que foi dado já conseguimos ver que:

T = 2 π ; ω = 1

Dessa forma o valor de a o será:

a o = 1 2 π ∫ 0 π 5   d t + ∫ π 2 π 10   d t

Então:

a o = 1 2 π 5 π + 10 2 π - π

a o = 15 π 2 π = 7.5

Passo 2

Agora o valor de a n nos dá:

a n = 2 2 π ∫ 0 π 5 cos ⁡ n t d t + ∫ π 2 π 10 cos ⁡ n t d t

a n = 1 π 5 n sin ⁡ n t 0 π + 10 n sin ⁡ n t π 2 π

a n = 5 n π sin ⁡ π n - sin ⁡ 0 + 2 sin ⁡ 2 π n - 2 sin ⁡ π n

Onde para n inteiro vemos que:

sin ⁡ 0 = sin ⁡ π n = sin ⁡ 2 π n = 0

Logo:

a n = 0

Passo 3

Agora para b n :

b n = 2 2 π ∫ 0 π 5 s in ⁡ n t d t + ∫ π 2 π 10 s in ⁡ n t d t

b n = 5 π n ( - cos ⁡ n t 0 π + 2 - cos ⁡ n t π 2 π

Isso será:

b n = 5 π n - cos ⁡ π n + cos ⁡ 0 - 2 cos ⁡ 2 π n + 2 cos ⁡ π n

b n = 5 π n - cos ⁡ π n + 1 - 2 cos ⁡ 2 π n + 2 cos ⁡ π n

O cosseno nós mantemos dessa forma pois quando n é par ele é diferente para quando ele é ímpar, o cosseno fica variando o sinal de - 1 para 1 alterando nossa conta.

Quando n par:

b n = 5 π n - 1 + 1 - 2 + 2 = 0

Quando n impar.

b n = 5 π n 1 + 1 - 2 - 2 = - 10 π n

Então tanto faz escrevermos b n da sua forma expandida ou dessa forma aqui abaixo.

f t = 7.5 + ∑ n = 1 ∞ 5 π n - cos ⁡ π n + 1 - 2 cos ⁡ 2 π n + 2 cos ⁡ π n s i n ⁡ ( n t )

f t = 7.5 - ∑ n = s o m e n t e   n ú m e r o s   i m p a r e s ∞ 10 π n   s i n ⁡ ( n t )

Isso nos dá o seguinte gráfico.

Resposta

a o = 7.5

a n = 0

b n = 5 π n - cos ⁡ π n + 1 - 2 cos ⁡ 2 π n + 2 cos ⁡ π n

Ver Outros Exercícios desse livro