Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 30

Determine v_o ( t ) , para todo t > 0 , no circuito da figura.

Passo 1

Vamos começar desenhando o circuito no domínio s (Laplace):

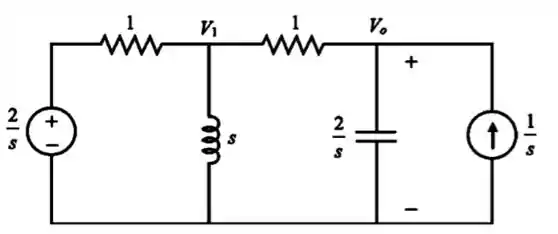
Passo 2

Agora, se a gente escrever a função degrau matematicamente, vai ser mais fácil de ver o que acontece em t > 0 e t < 0 .

u ( t ) = A AA t > 0 ,

u ( t ) = 0 AA t < 0 ,

Para todo t < 0 , tanto a fonte de tensão (curto) e de corrente (aberto) são iguais a zero, ou seja, i_L ( 0 ) = 0 A e v_o ( 0 ) = 0 V .

Passo 3

Então, vamos aplicar a Lei de Kirchhoff das correntes no nó V_1 .

(V_1 - (2)/(s))/(1) + (V_1)/(s) + (V_1 - V_o)/(1) = 0

s V_1 - 2 + V_1 + s V_1 - s V_o = 0

( 2 s + 1 ) V_1 - s V_o = 2

Passo 4

Aplicando a Lei de Kirchhoff das correntes no nó V_o também, teremos:

(V_o - V_1)/(1) + (V_o)/((2)/(s)) - (1)/(s) = 0

V_o - V_1 + (s V_o)/(2) - (1)/(s) = 0

- V_1 + (1 + (s)/(2)) V_o = (1)/(s)

V_1 = (1 + (s)/(2)) V_o - (1)/(s)

Passo 5

Se substituirmos o nosso V_1 nessa equação ( 2 s + 1 ) V_1 - s V_o = 2 , a gente acha o V_o em Laplace, daí é só passar pro domínio do tempo, vamo lá:

( 2 s + 1 ) [(1 + (s)/(2)) V_o - (1)/(s)] - s V_o = 2

( 2 s + 1 ) (1 + (s)/(2)) V_o - ( 2 s + 1 ) (1)/(s) - s V_o = 2

[2 s + 1 + s^2 + (s)/(2) - s] V_o = 2 + (2 + (1)/(s))

[s^2 + (3)/(2) s + 1] V_o = (4 s + 1)/(s)

[s^2 + 1.5 s + 1] V_o = (4 s + 1)/(s)

V_o = (4 s + 1)/(s [s^2 + 1.5 s + 1])

Basta abrir em frações parciais agora:

(4 s + 1)/(s [s^2 + 1.5 s + 1]) = (A)/(s) + (B s + C)/(s^2 + 1.5 s + 1)

4 s + 1 = A ( s^2 + 1.5 s + 1 ) + s ( B s + C )

4 s + 1 = A s^2 + 1.5 A s + A + B^2 + s C

4 s + 1 = ( A + B ) s^2 + ( 1.5 A + C ) s + A

Daí, igualando os termos constantes temos:

A = 1

Igualando os termos com s^2 :

A + B = 0

B = - A

B = - 1

Igualando os termos com s:

1.5 A + C = 4

1.5 ( 1 ) + C = 4

C = 2.5

Passo 6

Agora, vamos substituir A , B e C :

(4 s + 1)/(s [s^2 + 1.5 s + 1]) = (1)/(s) + (- s + 2.5)/(s^2 + 1.5 s + 1)

(4 s + 1)/(s [s^2 + 1.5 s + 1]) = (1)/(s) + (- s + 2.5)/((s + (3)/(4))^2 + ((sqrt(7))/(4))^2)

(4 s + 1)/(s [s^2 + 1.5 s + 1]) = (1)/(s) - [(s + (3)/(4) - 3.25)/((s + (3)/(4))^2 + ((sqrt(7))/(4))^2)]

(4 s + 1)/(s [s^2 + 1.5 s + 1]) = (1)/(s) - (s + (3)/(4))/((s + (3)/(4))^2 + ((sqrt(7))/(4))^2) + ((3.25)/(((sqrt(7))/(4))) ((sqrt(7))/(4)))/((s + (3)/(4)^())^2 + ((sqrt(7))/(4))^2)

Passo 7

Agora, com a tabela útil de transformadas de Laplace, conseguiremos resolver essa equação e passar ela do domínio s para o domínio do tempo:

t harr (1)/(s^2)

e^(- a t) c o s omega t harr (s + a)/(( s + a )^2 + omega^2)

e^(- a t) s i n omega t harr (omega)/(( s + a )^2 + omega^2)

Faremos a inversa:

v_o ( t ) = u ( t ) - e^(- (3)/(4) t) c o s ((sqrt(7))/(4) t) + 4.9135 s i n ((sqrt(7))/(4) t) , AA t > 0 .

Resposta

v_o ( t ) = u ( t ) - e^(- (3)/(4) t) c o s ((sqrt(7))/(4) t) + 4.9135 s i n ((sqrt(7))/(4) t) , AA t > 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Normalmente, podemos obter o circuito equivalente de Thévenin no domínio do tempo.a) verdadeiro b) falso
A tensão em um resistor com corrente i ( t ) no domínio s é s R I ( s ) . (a) verdadeiro (b) falso
Um circuito apresenta a função de transferência H s = s + 1 ( s - 2 ) ( s + 3 ) O circuito é estável.a) verdadeiro b) falso
Se a entrada para um sistema linear for δ ( t ) e a saída e - 2 t u ( t ) , a função de transferência do sistema será:a) 1 s + 2 b) 1 s - 2 c) s s + 2 d) s s - 2
A corrente através de um circuito R L em série com tensão de entrada v ( t ) é dada no domínio s como:a) V s R + 1 s L b) V ( s ) ( R + s L ) c) V s R + 1 s L d) V s R + s L