Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 29

Determine i ( t ) para t > 0 no circuito da figura.

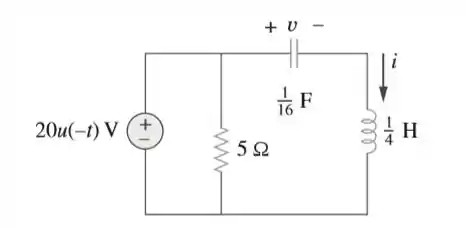
Passo 1

Em t < 0 temos 20 u ( - t ) = 20 V .

Vamos considerar que o circuito está em regime permanente em t < 0^() . Nesse caso, o capacitor age como um circuito aberto e o indutor, como um curto circuito.

Desenhando o circuito em t < 0 :

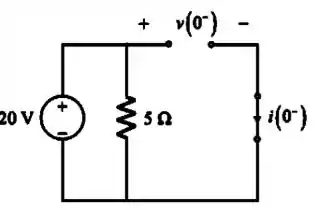
Passo 2

Vamos calcular i ( 0^- ) :

i ( 0^- ) = 0

Como no indutor não pode haver mudança repentina na corrente, então i ( 0^- ) = i ( 0^+ ) = 0 A

Vamos também calcular v ( 0^- ) :

v ( 0^- ) = 20 V

Como no capacitor não pode haver mudança repentina na tensão, então v ( 0^- ) = v ( 0^+ ) = 20 V

Passo 3

A fonte de tensão 20 u ( - t ) = 0 (curto circuito) para t > 0 .

Desenhando:

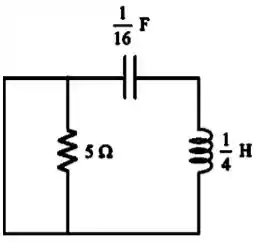
Passo 4

Vamos simplificar esse circuito porque aí temos um curto circuito. Vamos também desenhar logo no domínio de Laplace:

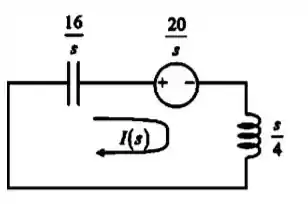
Passo 5

Aplicando a Lei de Kirchhoff das tensões:

(16)/(s) I ( s ) + (20)/(s) + (s)/(4) I ( s ) = 0

I ( s ) [(16)/(s) + (s)/(4)] = - (20)/(s)

I ( s ) [64 + s^2] = - (20)/(s) ( 4 s )

I ( s ) = - (80)/(s^2 + 8^2)

I ( s ) = - 10 ( (8)/(s^2 + 8^2) )

Passo 6

Agora vamos aplicar a transformada de Laplace inversa:

Sabendo que:

s i n omega t harr (omega)/(s^2 + omega^2)

Aplicando, vamos encontrar a corrente para t > 0 :

i ( t ) = - 10 s i n 8 t u ( t )

i ( t ) = 10 [- s i n 8 t] u ( t )

i ( t ) = 10 c o s ( 90 ° + 8 t ) u ( t ) A

Resposta

i ( t ) = 10 c o s ( 90 ° + 8 t ) u ( t ) A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais a seguir:(a) int_1^t u (lambda) d lambda (b) int_0^4 [ r (t - 1) ] d t (c) int_1^5 (t - 6)^2 * delta (t - 2) d t
Expresse os sinais a seguir em termos de funções de singularidade. av t = 0 , t0 - 5 , t0 bi t = 0 , t1 - 10,1t3 10,3t5 0 , t5 cx t = t - 1,1t2 1,2t3 4 - t , 3t4 0 , c a s oc o n t r á r i o á dy t =
Calcule as integrais a seguir envolvendo as funções de impulso: a∫ - ∞ ∞ 4 t 2 ⋅ δ t - 1 d t b∫ - ∞ ∞ 4 t 2 ⋅ cos ⁡ 2 π t ⋅ δ t - 0.5 d t
Esboce a forma de onda representada por i (t) = r (t) - r (t - 1) - u (t - 2) - r (t - 2) + r (t - 3) + u (t - 4)
Calcule as integrais a seguir:(a) int_(- oo)^(oo) e^(- 4 t^2) * delta (t - 2) d t (b) int_(- oo)^(oo) [ 5 * delta (t) + e^(- t) * delta (t) + cos (2 pi t) * delta (t) ] d t