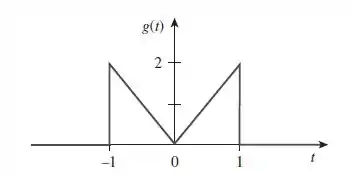
Determine a transformada de Fourier da forma de onda exibida na Figura .
Passo 1
Galerinha, podemos expressar essa função da seguinte maneira:
Vamos aplicar a transformada de Fourier:
Isso significa que realizaremos a soma das transformadas nos 2 intervalos da função.
Passo 2
Temos então que:
Vamos usar as seguintes relações trigonométricas exponenciais:
Assim:
Resposta
A transformada é igual a: