Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 15
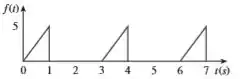
Determine a transformada de Laplace da função da Figura
Passo 1
A primeira coisa a se fazer aqui é escrever essas retas aí em forma de função. Ora, toda reta pode ser escrita assim:
Atenção! Essas retas verticais não são funções e, portanto, não precisam ser escritas. Não tem problema algum, pois vamos descrever futuramente a usando degrau e a própria definição de degrau já tem uma reta vertical:
Passo 2
Para a primeira reta crescente, sabemos dois pontos dela em particular: e . Então...
Então a primeira reta é
Passo 3
Para a terceira reta, sabemos que ela começa em e que ela é facilmente obtida deslocando a reta que já em encontramos em unidades pra direita em , o que equivale fazer...
Passo 4
Para a segunda reta, sabemos que ela começa em , ou seja precisamos deslocar unidades pra direita em , o que equivale fazer...
Passo 5
Com a equação das retas encontradas, a gente tem que descrever a figura em uma função usando o conceito de degraus...
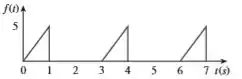
Bem, de até , a função vale e de até ela passa ser igual a equação da reta. Se a gente multiplicar então a equação da primeira reta por um degrau começando em ...
A gente ganha o que a gente falou aqui: “de até , a função vale e de até ela passa ser igual a equação da reta”. Afinal, o degrau tem a seguinte definição:
Assim, antes de , e depois de , o degrau vira e . Mas atenção! só vale até . Depois desse ponto para de ser essa reta e vira até :
- Parar de ser a reta crescente, significa que volta a ser somando nesse instante o negativo:
Perceba que antes de , nada mudou, pois , mas depois de , e vira , como queríamos.
Mas atenção novamente! A função não é a para sempre! Após ela volta a virar uma reta (dessa vez a da segunda rampa). O que significa adicionar :
Após ela volta a ser :
Acho que já pegou a ideia, ne? Após , ela vira a outra rampa...
Por último, após , ela volta a ser e fica pra sempre :
PRONTINHO! Como verificamos cada trecho (de indo de até ), a função está completamente descrita!
Passo 6
Finalmente, podemos fazer o que se pede: A transformada de Laplace.
Pois bem, a Laplace de uma função multiplicada por um degrau se calcula assim:
Então vamos tentar colocar todo mundo aí nesse formato:
Perceba que todos esses que já são positivo, já estão no formato que a gente quer :
Como e ...
Para os negativo, a gente vai usar o truque do tira e põe :
Então...
PRONTINHO .