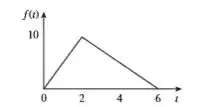
Determine a transformada de Laplace do sinal na figura

Para a primeira reta (crescente), sabemos dois pontos dela em particular: e . Então...

Então a primeira reta é

Para a segunda reta (decrescente) temos os pontos: e :

Isolando na segunda equação...

Então...

E

Então a segunda reta é...

Com a equação das retas encontradas, a gente tem que descrever a figura em uma função usando o conceito de degraus...

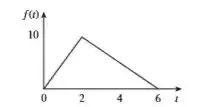
Bem, de até , a função vale e de até ela passa ser igual a equação da reta. Se a gente multiplicar então a equação da primeira reta por um degrau começando em ...

A gente ganha o que a gente falou aqui: “de até , a função vale e de até ela passa ser igual a equação da reta”. Afinal, o degrau tem a seguinte definição:

Assim, antes de , e depois de , o degrau vira e . Mas atenção! só vale até . Depois desse ponto para de ser essa reta e passa a ser a outra reta:

• Parar de ser a reta crescente, significa que volta a ser somando nesse instante o negativo:

Perceba que antes de , nada mudou, pois , mas depois de , e vira , como queríamos.

• Mas nesse mesmo instante que paramos de ser uma reta, a gente passa a ser outra, então...

Pode conferir:

Viu só! Depois de a função vira a reta decrescente.

Mas atenção novamente! A função não é a reta decrescente para sempre! Após ela para de ser essa reta novamente (). Como podemos parar uma função em notação de degrau? Isso mesmo, acrescentando o inverso no tempo de parada ():

PRONTINHO! Como verificamos cada trecho (de indo de até ), a função está completamente descrita!

Finalmente, podemos fazer o que se pede: calcular a transformada de Laplace da função (mas antes vamos só simplificar a função ):

Aplicando Laplace...

Toda vez que tivermos multiplicando, podemos pensar assim:

Então, como a transformada do degrau é ...

Essa primeira derivada é tranquila...

Para essa segunda derivada, podemos aplicar a regra da fração...

Fazendo o mesmo para essa última derivada...

Simplificando um pouquinho mais...