Obtenha as transformadas de Laplace das funções na figura.
Passo 1
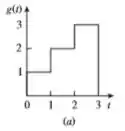
A gente pode escrever essa figura aí da seguinte maneira: em forma de degrau.
Esses números na frente de cada degrau são valores correspondentes ao tamanho do das barrinhas verticais. Por exemplo, em , temos um degrau de unidade (barra vertical), em , ele vai para subindo unidade novamente (barra vertical), em ela sobe para ( unidadi) e por fim... Em ela cai ficando para sempre! Saca?
Pode verificar se quiser:
Então a única função degrau que não é e sim é , logo...
Se , então e , mas os dois primeiros...
Como deveria ser de fato, saca?
Passo 2
Com isso em mãos, basta aplicar a transformada de Laplace em todo mundo :
Ora, a transformada do degrau é...
Então...