Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 22b
Determine as transformadas de Laplace das funções na figura:
Passo 1
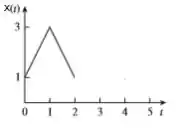
Bem, para começo de conversa, observe aqui que a função é periódica de período igual a :
Se a gente considerar como sendo apenas o trechinho que depois vai se repetir:
De acordo com a teoria de transformadas de funções periódicas, a transformada da função será:
Então agora temos que encontrar a transformada da função ! Bora?
Passo 2
Primeiramente, quem é a função de uma forma matematicamente falando? Bem, ela é um pedacinho de reta crescente até , e depois ela é uma reta decrescente até . Finalmente ele é depois disso eternamente, certo?
E quem são essas retas?
Bem, podemos encontrar a equação delas através de pontos conhecidos lembrando-se de que a equação da reta é
Os dois pontos conhecidos da primeira são e :
Da primeira tiramos que e da segunda tiramos que . Então...
Para a reta decrescente os pontos conhecidos são e
Onde tiramos dessa vez que e ...
Logo, podemos então falar que é...
Agora, para termos a Laplace dessa função, temos que coloca-la em notação de degrau! Bora?
Passo 3
Bem, perceba que antes de , a função é - não é falado no problema, mas sabemos disso já que só tem definição de em diante. Depois de , ela passa a ser a , podemos escrever isso em forma de degrau:
Mas ela não é a reta para sempre, afinal em , ela para de crescer se transforma em na :
OBS: Parar significa tornar igual a , por isso subtraímos , mas nesse mesmo momento, se torna reta decrescente, por isso adicionamos .
Depois de ela para de ser a reta decrescente novamente e se torna :
Prontinho! Depois de a é para todo o sempre! Pode verificar .
Passo 4
Finalmente podemos encontrar a Laplace de ...
Ora bolas, sabemos que a transformada de função vezes o degrau é da seguinte maneira:
Então precisamos encontrar esse formato aí em todas elas! O que vamos fazer é alterar esses números somando o para que se torne o que a gente quer...
Então, colocando em evidência...
Então, aplicando a fórmula...
Colocando todo mundo com o mesmo denominador...
Passo 5
Então, podemos concluir que a Laplace de funções periódicas como a é...