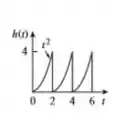
Determine as transformadas de Laplace das funções periódicas na figura
Passo 1
Bem, para começo de conversa, observe aqui que a função é periódica de período igual a :
Se a gente considerar como sendo apenas o trechinho que depois vai se repetir:
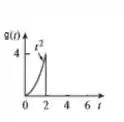
De acordo com a teoria de transformadas de funções periódicas, a transformada da função será:
Então agora temos que encontrar a transformada da função ! Bora?
Passo 2
A primeira coisa a se fazer aqui é construir essa em forma de degrau:
Ora, sabemos que a função é um pedacinho de parábola até , depois de ela vira , isso pode ser representado em degrau dessa maneira aqui:
Então prontinho! Função descrita !
Passo 3
Finalmente podemos encontrar a Laplace dessa :
Ora, a transformada de Laplace de uma função vezes o degrau é...
Então, no caso na nossa segunda Laplace...
Mas ...
Isolando quem a gente quer encontrar...
Mas veja que ainda surgiu que de forma análoga, a gente só sabe encontrar . Podemos então colocar esse e somar ao mesmo tempo:
Então, finalmente, podemos voltar para o cálculo da transformada da ...
Aplicando então a regra de transformada de função vezes o degrau...
Então...
Passo 4
Então, podemos falar que a transformada da função periódica é...