Elabore um problema, mais complexo do que o apresentado no Problema 14.10, para ajudar outros estudantes a entender melhor como determinar os gráficos de Bode de amplitude e de fase de uma determinada função de transferência em termos de . Inclua pelo menos uma raiz repetida de segunda ordem.
Passo 1
Galera, vamos resolver a seguinte questão:
“Esboce o gráfico de Bode para
Vamos escrever a equação na forma padrão:
A magnitude da função de transferência é:
A fase da função de transferência é:
Desenhando cada termo para a magnitude e a fase e adicionando eles graficamente, conseguimos ter as duas curvas abaixo
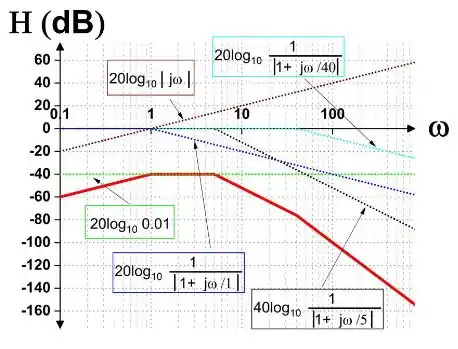
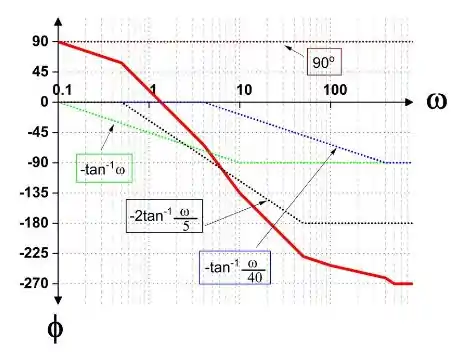
Resposta
Ei, a resposta está no passo a passo :)