Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 63

Faça o gráfico do espectro de amplitude do sinal f 2 t da figura 17.56b. Considere os primeiros cinco termos.

Passo 1

Primeiramente vamos atrás da figura que o enunciado está tratando que é a seguinte:

Pela simetria apresentada no gráfico podemos perceber que a nossa função é uma função par, logo, podemos obter alguns dados que são: T = 3 , ω = 2 π / 3 ,   b n = 0 . Além disso, nossa função f t será dada pela seguinte regra

f t = 1 ,     0 < t < 1 2 ,     1 < t < 1.5

Nossos coeficientes serão dados por

a 0 = 2 T ⋅ ∫ 0 t 2 f t d t = 2 3 ⋅ ∫ 0 1 1   d t + ∫ 1 1.5 2   d t = 4 3 ≈ 1 . 3 -

a n = 4 T ⋅ ∫ 0 T 2 f t ⋅ cos ⁡ n ω 0 t   d t = 4 3 ⋅ ∫ 0 1 cos ⁡ 2 n π t 3 d t + ∫ 1 1.5 2 ⋅ cos ⁡ 2 n π t 3 d t

a n = - 2 n π ⋅ sin ⁡ 2 n π 3

Sendo assim, nossa f 2 t será dada por

f 2 t = 4 3 - 2 π ⋅ ∑ n = 1 ∞ 1 n ⋅ sin ⁡ 2 n π 3 ⋅ cos ⁡ 2 n π 3

Assim, para transformar em magnitude a partir dos dados obtidos acima podemos fazer

A n = a n 2 + b n 2 = 2 n π ⋅ sin ⁡ 2 n π 3

Assim, nossos 5 primeiros termos serão

A 1 = 2 π ⋅ sin ⁡ 2 π 3 ≈ 0.5513

A 2 = 1 π ⋅ sin ⁡ 4 π 3 ≈ 0 . 2757

A 3 = 2 3 π ⋅ sin ⁡ 2 π = 0

A 4 = 1 2 π ⋅ sin ⁡ 8 π 3 ≈ 0 . 1375

Portanto, nosso gráfico de amplitude vai ser dado por

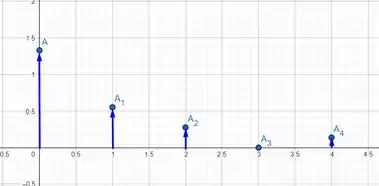
Resposta

Ver Outros Exercícios desse livro