Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 38

Determine a frequência de ressonância do circuito na Figura 14.78

Passo 1

Essa é uma questão de matemática pura, o curioso é que nem número tem kkk. Nós vamos fazer o circuito equivalente e as contas passo a passo, para achar uma expressão para frequência de ressonância ω , ok? Nós vamos tratar tudo como impedância e fazer as associações. Estamos trabalhando com números complexos e para facilitar vamos fazer de tudo para eliminar a unidade imaginária j e ir isolando o ω .

O circuito fasorial vai ser:

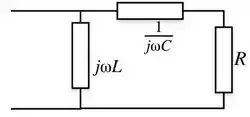
Então:

Z e q = j ω L   ∥ 1 j ω C + R

O ∥ na fórmula quer dizer “em paralelo”.

Desenvolvendo o paralelo para dois ramos fica:

Z e q = j ω L ⋅ 1 j ω C + R j ω L + 1 j ω C + R  

Z e q = j ω L j ω C + j ω L R j ω L + 1 j ω C + R

Simplificaremos e aplicaremos Identidade especial   1 j = - j :

Z e q = L C + j ω L R j ω L - j 1 ω C + R

Z e q = L C + j ω L R R + j ω L - 1 ω C

Agora temos dois dados no formato padrão de números complexos tanto no numerador quanto no denominador, ele tem a forma R e a l   + j ( a r g u m e n t o ) . Dessa forma, vamos realizar a divisão multiplicando a fração pelo conjugado do denominador. Vc também pode perceber que no fundo estamos multiplicando por 1, o que não altera o resultado. Nós estamos fazendo isso para poder retirar o j do denominador.

Z e q = L C + j ω L R R + j ω L - 1 ω C ⋅ R - j ω L - 1 ω C R - j ω L - 1 ω C

Vamos aplicar a distributiva, não se assuste com o tamanho, vamos simplificar muita coisa...

Z e q = L C R - L C j ω L - 1 ω C + j ω L R R - j j ω L R ω L - 1 ω C R 2 - j R ω L - 1 ω C + j R ω L - 1 ω C - j j ω L - 1 ω C 2

Agora temos vários componentes para simplificar e arrumar, tanto na parte de cima quanto na de baixo, lembrando que j j =   - 1 .

Z e q = L C R - j L C ω L - 1 ω C + j ω L R 2 + ω L R ω L - 1 ω C R 2 + ω L - 1 ω C 2

Veja que já não temos j no denominador.

Passo 2

Vamos continuar desenvolvendo, agora tentando simplificar a parte do numerador, vamos deixa-lo na forma padrão de número complexo R e a l   + j ( a r g u m e n t o ) .

Z e q = L C R + ω L R ω L - 1 ω C - j L C ω L - 1 ω C + j ω L R 2 R 2 + ω L - 1 ω C 2

Z e q = L C R + ω L R ω L - 1 ω C ⏞ R e a l + j ω L R 2 - L C ω L - 1 ω C ⏞ i m a g i n á r i o R 2 + ω L - 1 ω C 2

Passo 3

Agora vamos destrinchar a fração em duas. Agora isso é possível por que no denominador não temos mais o j .

Z e q =   L C R + ω L R ω L - 1 ω C ⏞ R e a l R 2 + ω L - 1 ω C 2   +   j ω L R 2 - L C ω L - 1 ω C ⏞ i m a g i n á r i o R 2 + ω L - 1 ω C 2  

Apesar de assustar pelo tamanho essa fórmula agora é exatamente a mesma coisa de:

Z   =   R + j X

Em que:

Z = I m p e d a n c i a

R = R e s i s t ê n c i a

X = R e a t â n c i a

Na frequência de ressonância a reatância X é zero, então tudo o que precisamos fazer agora é igualar a reatância X a zero. Observe que não teremos o j para nos “atrapalhar” e que não nos interessa mais o Z   e   o   R .

Passo 4

Como dito antes, na frequência de ressonância:

X = 0

Então:

ω L R 2 - L C ω L - 1 ω C R 2 + ω L - 1 ω C 2 = 0

O denominador irá anular com o zero.

ω L R 2 - L C ω L - 1 ω C = 0

ω L R 2 - L   C ω L + L ω C 2 = 0

Tirando o m . m . c , ficamos com:

C ω C 2 ω L R 2 - ω C 2 L ω L + C L C ω C 2           = 0

Mais uma vez o denominador irá anular com o zero.

C ω C 2 ω L R 2 - ω C 2 L ω L + C L = 0

ω 2 C 3 L R 2 - ω 2 C 2 L 2 + C L = 0

ω 2 ( C 3 L R 2 - C 2 L 2 ) = - C L

ω 2 =     - C L ( C 3 L R 2 - C 2 L 2 )    

ω 2 =     - C L C L ( C 2 R 2 - C L )    

ω 2 =     - 1 C 2 R 2 - C L    

Por conveniência multiplicamos por - 1 - 1 , para poder retirar o sinal negativo do numerador. Veja que isso não altera a desigualdade.

ω 2 =     - 1 C 2 R 2 - C L ⋅   - 1 - 1

ω 2 =     1 - C 2 R 2 + C L

ω 2 =     1 C L - C 2 R 2

ω =   1 C L - C 2 R 2  

E finalmente!

ω =   1 L C - R 2 C 2

Resposta

ω =   1 L C - R 2 C 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Demonstre que para um filtro passa-faixa, H s = s B s 2 + s B + ω 0 2,s = j ω Onde B = largura de banda do filtro e ω 0 é a frequência central
(b) De modo similar, demonstre que, para um filtro rejeita-faixa, H s = s 2 + ω 0 2 s 2 + s B + ω 0 2,s = j ω
Determine a frequência central e a largura de banda dos filtros passa-faixa na Figura 14.88Letra a)
Determine a frequência central e a largura de banda dos filtros passa-faixa na Figura 14.88Letra b)
Determine a largura de banda e a frequência de corte do filtro rejeita-faixa da Figura 14.89.