Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 95
A Figura mostra um oscilador Hartley. Demonstre que a frequência de oscilação é
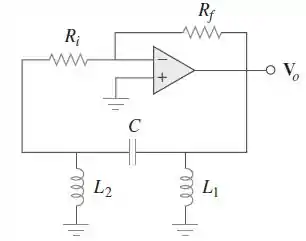
Passo 1
Pessoal, vamos olhar para a parte de feedback (a parte de baixo do circuito, com e ). Vamos calcular a impedância equivalente dessa parte:
Passo 2
A impedância deve ser puramente real. Assim, igualando a parte imaginária a zero:
Pronto! Conforme queríamos demonstrar! 😊
Resposta
Ei, a resposta está no passo a passo :)