Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 94

Projete um oscilador Colpitts que opere em 50   k H z .

Passo 1

Galera, a frequência de oscilação de um oscilador Colpitts pode ser escrita da seguinte forma:

f 0 = 1 2 π L C T

Onde C T = C 1 C 2 C 1 + C 2 . Vamos supor que C 1 = C 2 = 10   n F . Assim,

C T = 10 × 10 10 + 10

C T = 5   n F

Passo 2

Agora que temos o valor de C T e de f 0 , precisamos achar o valor de L .

f 0 = 1 2 π L C T

2 π 50 × 10 3 2 = 1 L C T

L = 1 2 π 50 × 10 3 2 5 × 10 - 9

L ≈ 2   m H

Vamos calcular o valor de X C 2 :

X C 2 = 1 ω 0 C 2 = 1 2 π f 0 C 2

X C 2 = 1 2 π 50 × 10 3 × 10 × 10 - 9

X C 2 = 1 π × 10 - 3

= 0,31847 × 10 3 = 318,47   Ω

Bom, o valor de R i deve obedecer a seguinte restrição: R i ≫ X C 2 ∴ R i ≫ 318,47   Ω . Seja R i = 20   k Ω . Para um ganho maior, R f > R i . Assim, vamos fazer que R f = 200   k Ω

G a n h o = V 0 V i = 1 + R f R i = 1 + 10 = 11

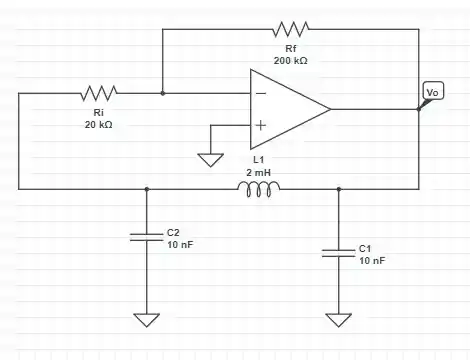
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro