Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 1.Problemas - Ex. 16

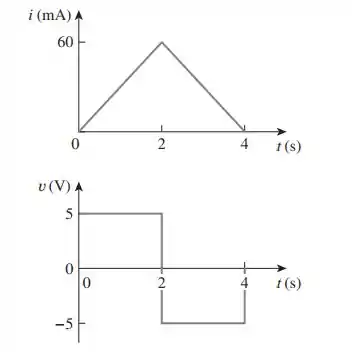
A figura 1.27 mostra a corrente e a tensão em um dispositivo.

  1. Esboce o gráfico da potência liberada para o dispositivo para t > 0 .
  2. Determine a energia total absorvida pelo dispositivo para o período 0 < t < 4 s .

Passo 1

Olha só: o gráfico da corrente sobe como uma reta, indo de 0 a 2 s , com a corrente indo de 0 a 60 m A . Assim, a inclinação da reta é:

60 m A 2 s = 30 m A s  

Por isso, a corrente nessa região pode ser escrita como:

i = 30 t

E a equação da reta no espaço após 2 s é:

i = 120 - 30 t

Por isso, para t entre 0 e 2 s :

P t = i U = 30 t   m A × 5   V = 150 t   m W

E para t > 2 s :

P t = i U = 120 - 30 t   m A × - 5 V = - 600 + 150 t   m W

Assim, o gráfico da potência será:

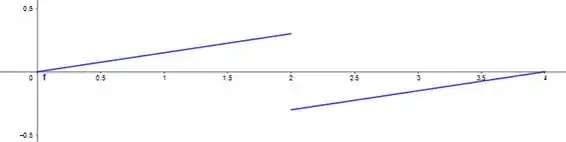
Esse gráfico está em W por s .

Passo 2

Para a energia, a gente só precisa integrar essa potência no tempo!

Para t entre 0 e 2 s :

E = ∫ 0 2 0,15 t d t = 0,15 t 2 2 0 2 = 0,3 J  

Para t entre 2 e 4 s :

E = ∫ 2 4 - 0,6 + 0,15 t d t = 0,15 t 2 2 - 0,6 t 2 4

E = 0,15 × 4 2 2 - 0,6 × 4 - 0,15 × 2 2 2 + 0,6 × 2

E = - 0,3 J

No total, temos uma energia igual a 0 . Isso se explica pelo fato de que a tensão fica em parte positiva e em parte negativa.

Resposta

  1. Gráfico.
  2. 0J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule i e a potência entregue ao resistor.
A tensāo sobre um resistor de 10 k Ω é 50V . Calcule (a) a condutância, (b) a corrente e (c) a potência mínima do resistor.
A potência instantânea absorvida por um resistor ê 4 sen 2 377 tW . Se a corrente é 40 sen 377 tm A , calcule v e R .
Calcule a energia consumida por uma torradeira com resistência de 12Ω, que opera a 120 V por 10 s.
Um elemento de dois terminais absorve uma energia w como mostrado. Se a corrente que entra pelo terminal positivo éi= 100 cos ⁡ ( 1000 π t )m A CaIcule a tensão sobre 0 elemento em t=1m s e em t=4m s