Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 3.Problemas - Ex. 17
Na Figura do Prob. 3.16. considere que e conecte um resistor R entre os terminais c-d. Mostre que a resistência vista dos terminais de entrada a-b e = -R. (A Figura do Prob. 3.16 então converte resistências positivas para resistências negativas).
Passo 1
Dado o circuito:
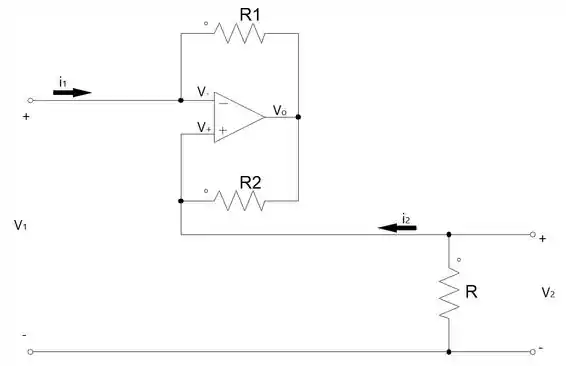
Na questão anterior, vimos que e que . Então vamos usar essas informações a nosso favor nessa questão.
Passo 2
Se e , temos .
Agora, considerando , podemos discorrer sobre essa igualdade. Mas antes, temos que fazer uma pequena mudança, para analise de malhas, essa igualdade não se satisfaz, pois, as mesmas estão em polaridades opostas.
Passo 3
Por fim:
, se .
.
Resposta
Exercícios de Livros Relacionados
Use os resultados da Tabela 4.2 para prever os valores de v1 e v2 se R1 e R3 aumentarem para 10% acima de seus valores nominais e R2 e R4 diminuírem para 10% abaixo de seus valores nominais. Ig1 e Ig2
O amp op no circuito da Figura P5.19 é ideal.Qual é a configuração desse circuito amp op?Determine vo em termos de vs.Determine a faixa de valores para vs tal que vo não sature e o amp op permaneça em
O amp op no circuito mostrado na Figura P5.10 é ideal. O resistor ajustável RD tem um valor máximo de 100 kV, e o valor de a está restrito à faixa de 0,2 # a # 1. Calcule a faixa de vo se vg = 40 mV.b
O amp op no circuito mostrado na Figura P5.20 é ideal.a) Calcule vo quando vg = 4 V. b) Especifique a faixa de valores de vg de modo que o amp op opere de modo linear.c) Admita que vg seja igual a 2 V