Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 70

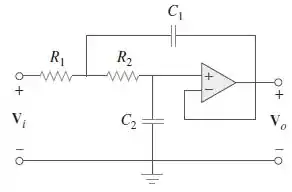
Um filtro ativo de segunda ordem conhecido como filtro Butterworth é mostrado na Figura 14.95 .

  1. Determine a função de transferência V 0 V i ;
  2. Demonstre que se trata de um filtro passa-baixas

Passo 1

Vamos pra letra (a), galera. Aplicando a lei dos nós no nó 1, temos:

V 1 - V i R 1 + V 1 - V 0 R 2 + V 1 - V 0 1 s C 1 = 0

V 1 1 R 1 + 1 R 2 + s C 1 = V i R 1 + V 0 s C 1 + 1 R 2

Multiplicando a equação por R 1 R 2 :

V 1 R 2 + R 1 + s C 1 R 1 R 2 = V i R 2 + V 0 s C 1 R 1 R 2 + R 1 … 1

Aplicando a lei dos nós no terminal não-inversor:

V 0 - V 1 R 2 + V 0 1 s C 2 = 0

V 1 = 1 + s C 2 R 2 V 0 … 2

Substituindo a equação ( 2 ) a equação ( 1 ) :

1 + s C 2 R 2 R 2 + R 1 + s C 1 R 1 R 2 = V i R 2 + V 0 s C 1 R 1 R 2 + R 1

Simplificando a equação,

s 2 R 1 R 2 2 C 1 C 2 + s R 1 R 2 C 2 + R 2 2 C 2 + R 2 V 0 = V i R 2

A função de transferência é igual a:

H s = V 0 V i = R 2 s 2 R 1 R 2 2 C 1 C 2 + s R 1 R 2 C 2 + R 2 2 C 2 + R 2

H s = 1 s 2 R 1 R 2 C 1 C 2 + s R 1 C 2 + R 2 C 2 + 1

Passo 2

Agora a letra (b). Colocando ω (ou s ) igual a zero e ∞ , podemos determinar o tipo de filtro. Logo,

H 0 = 1

H ∞ = 0

Os valores de H ( 0 ) e H ( ∞ ) mostram que o circuito é um filtro passa-baixa.

Resposta

  1. H s = 1 s 2 R 1 R 2 C 1 C 2 + s R 1 C 2 + R 2 C 2 + 1
  2. Temos um filtro passa-baixa.
Ver Outros Exercícios desse livro