Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 5
5. As respostas de um circuito em série são
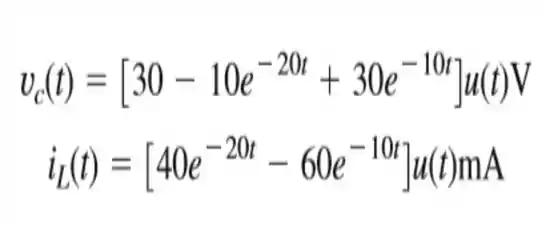
Onde e são respectivamente a tensão no capacitor e a corrente no indutor. Determine os valores de , e .
Passo 1
Vamos começar com a equação de malha generalizada para uma rede em série. Podemos agrupar as condições iniciais e com a fonte no loop, pois tudo o que estamos buscando atualmente são os valores de e .
Essa grandiosa equação pode ser reescrita como...
Os valores de virão das raízes da equação do denominador. Já sabemos que eles são iguais a e . Observamos, no entanto, que isso nos dará apenas duas equações. Obviamente, precisamos de um terço, e isso virá do conhecimento da corrente através do capacitor e da tensão através dele.
Passo 2
Bora então, trabalhar com a equação abaixo...
Como já sabemos os valores das raízes dessa equação...
Ou seja,
E também podemos fazer uso da reguinte relação:
Como...
Então...
Passo 3
Pra finalizar, temos a seguinte relação...
No caso...
Mas sabemos que...
E que...