Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 66
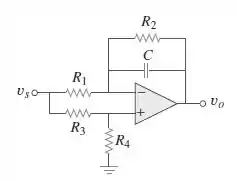
Um filtro de primeira ordem “genérico” é exposto na Figura .
- Demonstre que a função de transferência é
- Que condição deve ser satisfeita para o circuito operar como um filtro passa-altas?
- Que condição deve ser satisfeita para o circuito operar como um filtro passa-baixas?
Passo 1
Galera, no terminal positivo do amplificador, aplicando o divisor de tensão, temos:
Aplicando a lei dos nós no terminal negativo,
Ou,
Substituindo a equação na equação , temos:
Dividindo toda a equação por , temos:
Assim, a função de transferência do filtro é igual a:
Passo 2
Na letra (b) queremos saber que condição deve ser satisfeita para o circuito operar como um filtro passa-altas. Isso vai acontecer quando:
Passo 3
Na letra (c) queremos saber que condição deve ser satisfeita para o circuito operar como um filtro passa-baixas. Isso vai acontecer quando:
Isso acontece quando tende ao infinito!