Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 16

A forma de onda da Figura 17.55 a possui a seguinte série de Fourier

v 1 t = 1 2 - 4 π 2 cos ⁡ π t + 1 9 cos ⁡ 3 π t + 1 25 cos ⁡ 5 π t + …   V

Obtenha a série de Fourier de v 2 t na Figura 17.55 b .

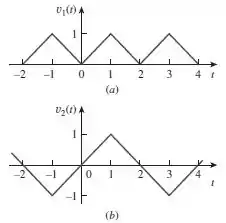
Passo 1

Vamos lá, galera! Deslocando v 1 em 0,5 para a esquerda, produziremos uma forma de onda v x da seguinte forma:

v x t = v 1 ( t + 0,5 )

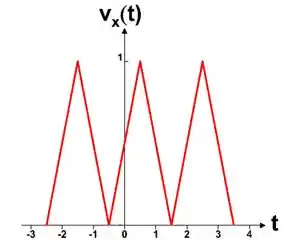
Expandindo o eixo do tempo, multiplicando a variável t por 0,5 , temos uma forma de onda v y :

v y t = v x 0,5 t

v y t = v 1 ( 0,5 t + 0,5 )

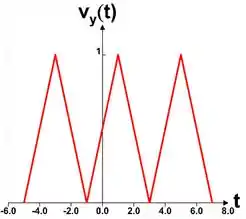
Passo 2

Deslocando na vertical v y em 0,5 , nós teremos a onda v z resultante:

v z t = v y t - 0,5

v z t = v 1 0,5 t + 0,5 - 0,5

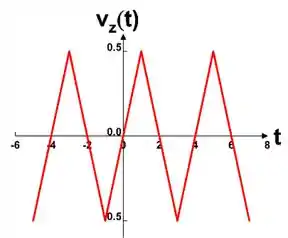
Multiplicando a amplitude de v z por 2 , teremos v 2 igual a:

v 2 t = 2 v z

v 2 t = 2 v 1 0,5 t + 0,5 - 1 … ( 1 )

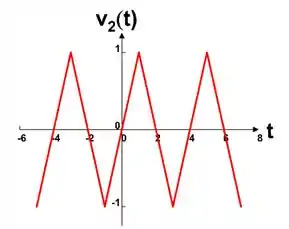
Passo 3

Dada a série de Fourier de v 1 ( t ) , podemos encontrar a série para v 1 ( 0,5 t + 0,5 ) substituindo cada t por 0,5 t + 0,5 :

v 1 0,5 t + 0,5 = 0,5 - 4 π 2 cos ⁡ 0,5 π t + 0,5 π + 1 9 cos ⁡ 3 0,5 π t + 0,5 π + 1 25 cos ⁡ 5 0,5 π t + 0,5 π + …

v 1 0,5 t + 0,5 = 0,5 - 4 π 2 s e n 0,5 π t + 1 9 s e n 3 0,5 π t + 1 25 s e n 5 0,5 π t + …

Substituindo na equação ( 1 ) ,

v 2 t = 2 0,5 - 4 π 2 s e n 0,5 π t + 1 9 s e n 3 0,5 π t + 1 25 s e n 5 0,5 π t + … - 1

v 2 t - 8 π 2 s e n 0,5 π t + 1 9 s e n 3 0,5 π t + 1 25 s e n 5 0,5 π t + …

Como a função v 2 é uma função ímpar, não há termo a 0 ou termos cosseno. Logo, a resposta faz sentido.

Resposta

A série é igual a:

v 2 t - 8 π 2 s e n 0,5 π t + 1 9 s e n 3 0,5 π t + 1 25 s e n 5 0,5 π t + …

Ver Outros Exercícios desse livro