Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 48
Uma fonte conectada em estrela equilibrada e de sequência positiva tem = 240 0 V RMS e alimenta uma carga conectada em triângulo desequilibrada por meio de uma linha de transmissão de impedância 2 + j3 por fase.
(a) Calcule as correntes de linha para = 40 + j15, = 60 e = 18 – j12 .
(b) Determine a potência complexa fornecida pela fonte.
Passo 1
Primeiro vamos entender o problema. Temos que carga em delta e uma fonte em estrela, então vamos converter a carga de delta para estrela. De tal modo que:
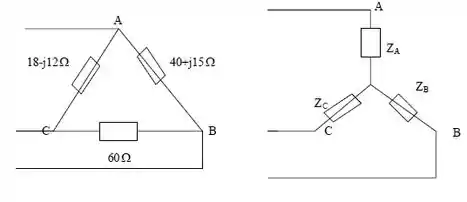
Lembre-se que, a carga está desequilibrada então não podemos simplesmente dividir por 3, temos que usar a outra relação.
Desse modo,
Passo 2
Agora podemos usar análise de malha para calcular as correntes de linha, o sistema fica:
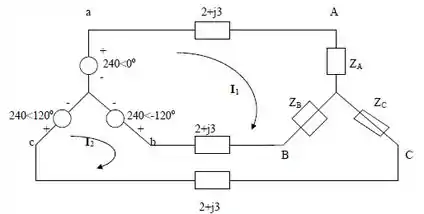
Aplicando LKV. Para a malha 1:
ou,
Para a malha 2:
ou,
Resolvendo o sistema para a malha 1 e 2, temos
Passo 3
A questão nos pede a corrente de linha. Note que,
Passo 4
Para o item b) que pede a potência da fonte podemos calcular a potência de cada fase e somar, assim terá a potência fornecida pela fonte. Sabendo que
Então
Logo, a potência complexa fornecida pela fonte é