Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 49

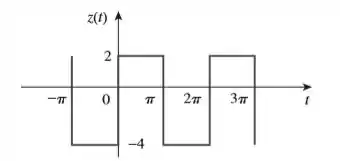
  1. Para a forma de onde periódica, determine o valor R M S .
  2. Use os cinco primeiros harmônicos da série de Fourier para determinar o valor eficaz do sinal.
  3. Calcule o Erro Percentual no Valor de R M S estimado de z t se

%   e r r o = v a l o r   e s t i m a d o v a l o r   e x a t o - 1 × 100

Passo 1

L e t r a   A

Poxa, a R M S é dada pela fórmula:

z r m s = 1 L ∫ 0 L z 2 t d t

Se a gente perceber que o L vale 2 π (período), e que a função tem diferentes valores de 0 a   π   e de π a 2 π ....

z r m s = 1 2 π ∫ 0 π z 2 t d t + ∫ π 2 π z 2 t d t   →

Substituindo esses valores da função...

z r m s = 1 2 π ∫ 0 π 2 2 d t + ∫ π 2 π - 4 2 d t   →

z r m s = 1 2 π 4 ∫ 0 π d t + 16 ∫ π 2 π d t   →

z r m s = 1 2 π 4 π - 0 + 16 2 π - π   →

z r m s = 1 2 π 20 π   →

z r m s = 10 = 3,162  

Passo 2

L e t r a   B

Já vimos que z t pode ser dado pela série de Fourier da seguinte forma

z t = 1 + 1 2 ∑ n = 1 ∞ 144 n 2 π 2     ( o u   0   s e   n   f o r   p a r )

E ainda que o z r m s pode ser encontrado ora pela definição po passo anterior, ou por...

z r m s = 1 L ∫ 0 L z 2 t d t = a 0 2 + 1 2 ∑ n = 1 ∞ a n 2 + b n 2   →

Então...

z r m s = 1 + 1 2 ∑ n = 1 ∞ 144 n 2 π 2   ( o u   0   s e   n   f o r   p a r )   →

Substituindo os 5 primeiros...

z r m s = 1 + 144 2 1 1 2 π 2 + 0 + 1 3 2 π 2 + 0 + 1 5 2 π 2   →

z r m s = 9,396   →

Z r m s = 3,065

Passo 3

L e t r a   C

Ora, pois...

%   e r r o = v a l o r   e s t i m a d o v a l o r   e x a t o - 1 × 100

O valor estimado é o valor que encontramos em B enquanto que o valor real é o de A :

%   e r r o = 3,065 3,162 - 1 × 100

%   e r r o = - 3,068 %

Resposta

z r m s = 3,162  

Z r m s ( e s t i m a d o ) = 3,065

%   e r r o = - 3,068 %

Ver Outros Exercícios desse livro