Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 3
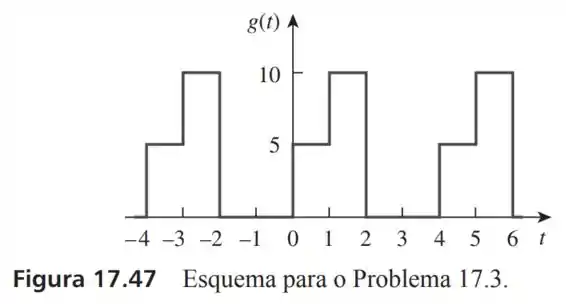
3- Forneça os coeficientes de Fourier e da forma de onda na Figura . Represente graficamente os expectros de amplitude e de fase.
Passo 1
Pelo gráfico podemos tirar que:
E então:
E as funções que essa onda tem dentro do período de são:
E cada termo pode ser desenvolvido da seguinte forma:
Passo 2
Então:
Passo 3
Agora para o valor de .
Como então:
sendo números inteiros temos qualquer :
Uma vez que
Onde para par temos . Exemplo, para :
E para teremos:
E para teremos:
Então teremos:
Passo 4
Agora :
Como
Então teremos:
Poderíamos também abordar aqui que mas vamos deixar dessa maneira.
Passo 5
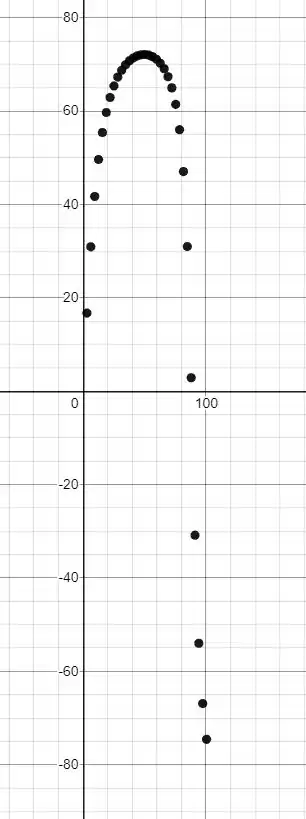
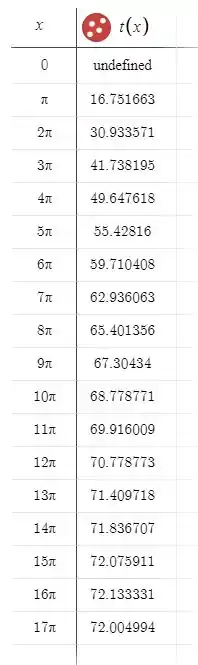
Plotando para pontos temos:
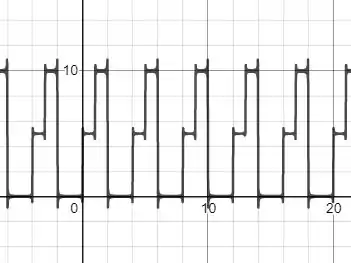
O que mostra que estamos certos.
Tabela para :
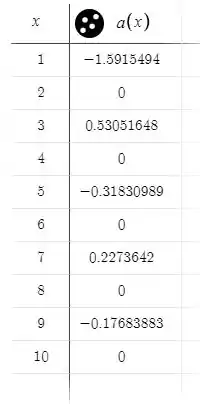
Tabela para :
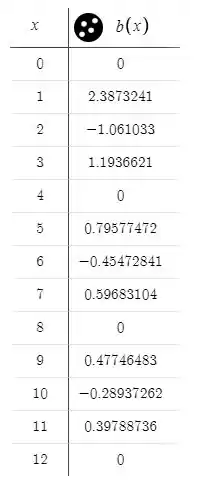
Passo 6
Agora para fase e frequência temos que fazer:
Amplitude:
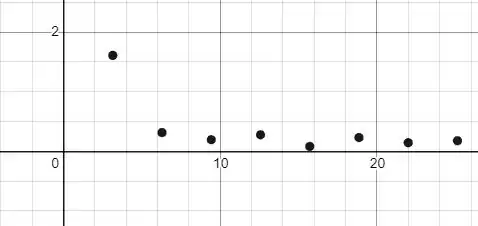
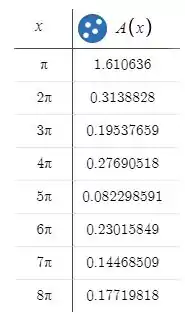
Gráfico da fase:
