Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 24
Na função periódica da Figura ,
- Determine os coeficientes e da série de Fourier trigonométrica.
- Calcule a magnitude e a fase da componente de que possui
- Use os quatro primeiros termos não nulos para estimar
- Demonstre que
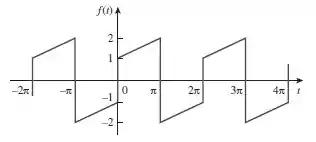
Passo 1
Vamos para a letra (a), galera! Notem que a função é uma função ímpar e isso pode ser provado, por exemplo, por e :
Da descrição do problema, temos:
Nós sabemos que os coeficientes para uma função ímpar, temos:
A função no intervalo pode ser definida usando a equação da reta entre dois pontos: :
Passo 2
Nós podemos determinar agora:
A primeira integral pode ser resolvida:
Portanto,
Para , temos:
Passo 3
Vamos para a letra (b). Como nós sabemos, . Para , temos:
Agora, podemos determinar os coeficientes!
A magnitude é igual a:
A fase é igual a:
Passo 4
Na letra (c), queremos estimar o a partir dos quatro primeiros termos não nulos. Assim,
Portanto, temos:
Finalmente, temos:
Passo 5
Por fim, a letra (d). Podemos aproximar a por
Assim,