Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 59
A série de Fourier complexa da função na Figura é
Determine a série de Fourier complexa da função da Figura .
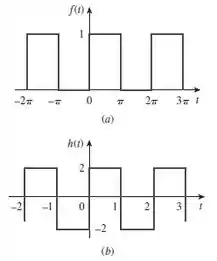
Passo 1
Vamos lá, galera! Para chegarmos ao gráfico da letra (b), precisamos multiplicar a variável por , ou seja, os valores do eixo horizontal serão divididos por .
Para termos a amplitude da função indo de a , precisamos que duas coisas ocorram: a amplitude de seja multiplicada por e que ocorra um deslocamento vertical, para baixo, de duas unidades. Logo,
Assim, escrevendo a série de Fourier:
Resposta
A série é igual a: