Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 22
a) Mostre que a corrente no k-ésimo ramo do circuito da Figura P3.22(a) é igual à correente da fonte vezes a condutância do k-ésimo ramo, dividida pela soma das condutâncias, isto é,
b) Use o resultado derivado em (a) para calcular a corrente no resistor de no circuito da Figura P3.22(b).
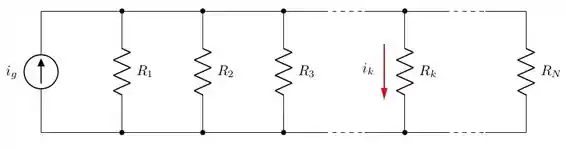
Figura 3.22 (a)
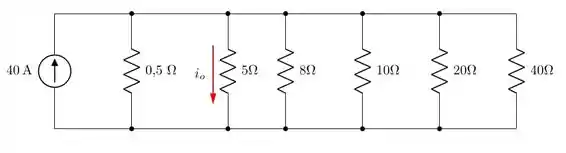
Figura 3.22 (b)
Passo 1
Show de bola, galera! Vamos terminar esta seção deste capítulo com o pé direito, “matando” essa questão que é “mamão com açúcar”. Vamos fazê-la da seguinte maneira: 1 passo para cada letra.
Passo 2
a)
Vamos olhar para a figura abaixo. É possível perceber uma característica entre os resistores: Todos estão em paralelo. Isso significa que a queda de tensão em cada um é a mesma. Assim, vamos chamar essa tensão de . Paralelamente (olha o trocadilho aqui) percebemos que também podemos fazer uso da Lei de Kirchhoff das Correntes da seguinte maneira: A soma da corrente que entra () é igual a soma das correntes que saem (a corrente em cada ramo).
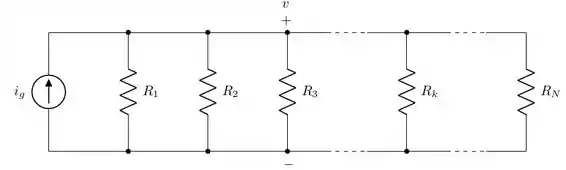
Então, vamos expressar isso numa fórmula matemática:
No entanto, o enunciado da questão está mostrando o resultado em função da condutância que é o inverso da resistência. Sendo assim, vamos transformar a expressão anterior usando este fato de uma grandeza ser a inversa da outra:
Show!
Então, isolando na equação anterior, obtemos
Passo 3
Agora, vamos pensar no seguinte:
A corrente no resistor 1 é dada por ; a corrente no resistor 2 é dada por ; e assim sucessivamente. Logo, é natural pensarmos que a corrente no k-ésimo ramo será dada por .
Então, vamos expressar como na expressão anterior, mas ao invés de usar , vamos usar o resultado do Passo 2:
Passo 4
b)
Uma vez que encontramos a fórmula do termo geral, tudo o que temos que fazer é substituir valores, mas temos que tomar cuidado com um pequeno detalhe: A resistência do k-ésimo termo é , o que significa que a condutância será o inverso deste valor, ou seja, , assim como as demais resistências:
E assim, chegamos ao final desta seção. Vamos para a próxima?!