Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 19

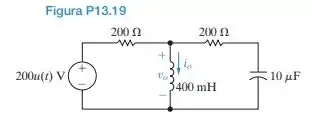
Não há nenhuma energia armazenada no circuito da Figura P13.19, em t = 0 - .

a) Use o método das tensões de nó para determinar i 0 .

b) Determine a expressão no domínio do tempo para v 0 .

c) Suas respostas em (a) e (b) fazem sentido em termos do comportamento conhecido do circuito? Explique.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Podemos demonstrar o circuito de acordo com a seguinte ilustração:

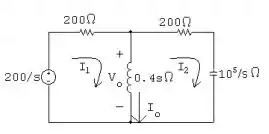
    2. Com isso, temos:

    200 i 1 + 0,4 s I 1 - I 2 = 200 s ;

    200 I 2 + 10 5 s I 2 + 0,4 s I 1 - I 2 = 0 ;

    Isolando e desenvolvendo os termos nesse sistema, temos que:

    I 2 = 0,5 s s 2 + 500 s + 125000

    I 1 = 0,5 ( s 2 + 500 s + 25 x 10 4 ) s ( s 2 + 500 s + 125000 )

    Aplicando as componentes de K, encontramos que:

    K 1 = 1 ; K 2 = 0,5 / - 180 ° = - 0,5

    Por fim:

    i 0 t = 1 - 1 e - 250 t c p s 250 t u t A

    Passo 2

  2. Sabemos que:

    3. V 0 = 0,4 I 0

    Logo:

    V 0 = 100 ( s + 500 ) s 2 + 500 s + 125000

    Aplicando as componentes de K, encontramos que:

    K 1 = 70,71 / - 45 °

    Por fim:

    v 0 t = 141,42 e - 250 t c o s ⁡ ( 250 t - 45 ° ) u t V

  3. Para t = 0 + :

v 0 0 + = 100 V = 141,42 cos ⁡ - 45 ° ; I 0 0 + = 0

Observando, percebemos que ambos os valores concordam com a solução para v 0 e i 0 .

Resposta

  1. Item a:

    2. i 0 t = 1 - 1 e - 250 t c p s 250 t u t A

  2. Item b:

    3. v 0 t = 141,42 e - 250 t c o s ⁡ ( 250 t - 45 ° ) u t V

  3. Item c: Observando, percebemos que ambos os valores concordam com a solução para v 0 e i 0 .