Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 59

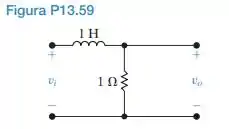
Um pulso de tensão retangular, v i   =   [ u ( t )   -   u ( t   -   1 ) ]   V , é aplicado ao circuito da Figura P13.59. Use a integral de convolução para determinar vo.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

Analisando o circuito acima, temos que:

H s = V 0 V i = 1 s + 1 → h t = e - t

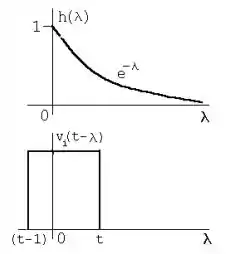
Portanto, para um tempo entre 0 e 1, temos que:

Passo 2

Temos então que a integral de convolução se comporta da seguinte forma:

v 0 = ∫ 0 t e - λ d λ = 1 - e - t V

Já para tempo entre 1 e ∞ , temos:

v 0 = ∫ t - 1 t e - λ d λ = e - 1 e - t V

Resposta

Para 0 ≤ t ≤ 1 :

v 0 = ∫ 0 t e - λ d λ = 1 - e - t V

Para 1 ≤ t ≤ ∞ :

v 0 = ∫ t - 1 t e - λ d λ = e - 1 e - t V

Exercícios de Livros Relacionados

Em um circuito R L C ,R = 20 ,L = 40 H ,C = 1 F .O circuito sofre uma aplicação de escala na amplitude de 10 e na frequência de 1 0 5 . Calcule os novos valores dos elementos.
Calcule os valores de R, L e C que resultarão em, respectivamente, R = 12 k, L = 40 mH e C = 300 nF quando houver a aplicação de fator de escala de amplitude 800 e fator de escala de frequência 1.000.
O circuito mostrado na figura tem impedância Z ( s ) = 1000 ( s + 1 ) ( s + 1 + j 50 ) ( s + 1 - j 50 ) ,s = j ω Determine: Os valores de R ,L ,CeG Os valores dos elementos que farão que a frequência
Um circuito R L C em série possui R = 10 Ω ,ω o = 40r a d / seB = 5r a d / s . Determine LeC quando o circuito sofre uma aplicação de escala: Na amplitude por um fator 600 . Na frequência por um fator
Observe o circuito da figura. Determine Z e n t ( s ) Aplique fatores de escala K m = 10eK f = 100 aos elementos. Determine Z e n t ( s )eω o .