Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 44

Obtenha a convolução dos pares de sinais nas figuras.

a)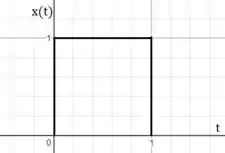

b)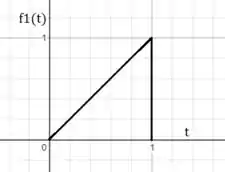

Passo 1

a) E novamente vamos “deslizar” o gráfico de x ( t ) sobre o gráfico de h ( t ) e calcular a integral de convolução para cada intervalo em que os gráficos são sobrepostos belezinha?

Para t < 0 , não há sobreposição dos gráficos, portanto, y t = 0

Para 0 < t < 1 , há sobreposição dos gráficos entre 0 e t ' , sendo que nesse intervalo, x t = 1 e h t = 1 . Então:

y t = ∫ 0 t ' 1 . 1   d t

y t = t

Para 1 < t < 2 , há sobreposição entre t ' - 1 e 1 (com x t e h ( t ) valendo 1) e depois entre 1 e t ' (com x ( t ) valendo 1 e h ( t ) valendo - 1 ):

y t = ∫ t ' - 1 1 1.1   d t + ∫ 1 t ' - 1.1   d t

y t = 3 - 2 t

Passo 2

Por fim, para o intervalo 2 < t < 3 , a sobreposição dos gráficos é dada de modo que a integral de convolução são:

y t = ∫ t ' - 1 2 - 1 . 1   d t

y t = t - 3

Já para t > 3 , não há sobreposição dos gráficos, então y t = 0

Portanto:

y t = t ,   0 < t < 1 - 2 t + 3 ,   1 < t < 2 t - 3 ,   2 < t < 3 0 ,   c a s o   c o n t r á r i o

Passo 3

b) Para o intervalo t < 2 , não há sobreposição dos gráficos, então, y t = 0 nesse intervalo.

Para 2 < t < 3 , os gráficos se sobrepõem de 2 até t ' :

y t = ∫ 2 t ' 1 . ( t ' - t )   d t

y t = t 2 2 - 2 t + 2

Para 3 < t < 5 , os gráficos se sobrepõem de t ' - 1 até t ' :

y t = ∫ t ' - 1 t ' 1 . ( t ' - t )   d t

y t = 1 2

Por fim, para 5 < t < 6

y t = ∫ t ' - 1 5 1 . ( t ' - t )   d t

y t = - t 2 2 + 5 t - 12

Para t > 6 , não há sobreposição dos gráficos, então y t = 0

Portanto:

y t = t 2 2 - 2 t + 2 ,   2 < t < 3 1 2 ,   3 < t < 5 - t 2 2 + 5 t - 12 ,   5 < t < 6 0 ,   c a s o   c o n t r á r i o

Resposta

a)

y t = t ,   0 < t < 1 - 2 t + 3 ,   1 < t < 2 t - 3 ,   2 < t < 3 0 ,   c a s o   c o n t r á r i o

b) y t = t 2 2 - 2 t + 2 ,   2 < t < 3 1 2 ,   3 < t < 5 - t 2 2 + 5 t - 12 ,   5 < t < 6 0 ,   c a s o   c o n t r á r i o

Ver Outros Exercícios desse livro