Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 63
Obtenha o equivalente de Norton do circuito representado na Figura 10.106 nos terminais a-b.
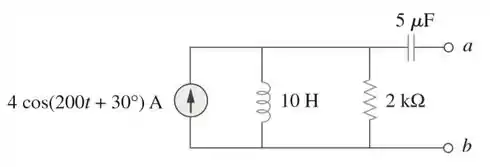
Passo 1
Vamos lá galera! Em questões de Thevenin ou Nortón, um dos macetes mais importantes é saber trabalhar para isolar as fontes e achar as impedâncias equivalentes! Primerio, vamos transformar o circuito para o domínio da frequência!
Passo 2
Para acharmos a impedância equivalente para Norton, usaremos o circuito abaixo:
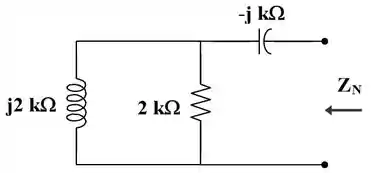
Para acharmos a corrente de Norton, usaremos o circuito abaixo!
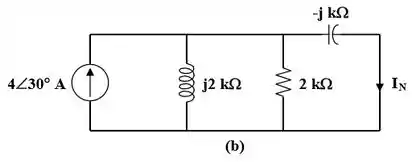
Pelo principio de divisão de corrente,
Resposta
Exercícios de Livros Relacionados
Consulte o circuito da Figura 10.49. A impedância equivalente de Norton nos terminais a-b é: - j 4Ω b) - j 2Ω c) j 2Ω d) j 4Ω
Consulte o circuito da Figura 10.49. A impedância equivalente de Norton nos terminais a-b é: - j 4Ω b) - j 2Ω c) j 2Ω d) j 4Ω
Consulte o circuito da Figura 10.47 e observe que as duas fontes não têm a mesma frequência. A corrente i x t pode ser obtida por:Transformação de fontesTeorema da superposiçãoPSpice
No circuito da Figura 10.48, a tensão de Thévenin nos terminais a-b é: 3.535 ∠ - 45 °V b) 3.535 ∠ 45 °V c) 7.071 ∠ - 45 °V d) 7.071 ∠ 45 °V
Para o circuito da Figura 10.48, a impedância de Thévenin nos terminais a-b é: 1 Ω b) 0.5 - j 0.5Ω c) 0.5 + j 0.5Ω d) 1 + j 2Ω e) 1 - j 2Ω