Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 48
48. Determine no circuito da figura usando a superposição.
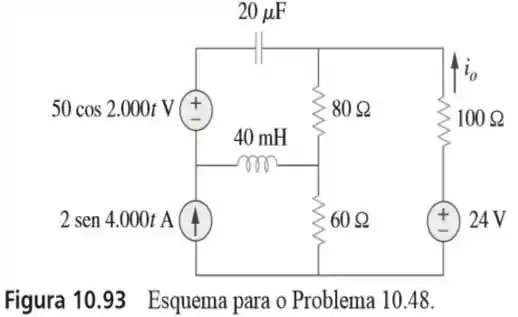
Passo 1
Fala galerinha! Bora pra mais um probleminha sobre superposição em circuitos .
Olha só! Na figura do enunciado, há a presença de uma fonte de corrente alternada, uma fonte de tensão alternada e outra fonte de tensão, dessa vez contínua.
O que precisamos fazer pra esse caso, é analisar a influência isolada de cada fonte no circuito. Ou seja, iremos considerar cada fonte separadamente, e a corrente elétrica total em qualquer ramo do circuito é igual a soma algébrica das tensões produzidas por cada fonte atuando separadamente.
Vamos então, por a mão na massa.
Passo 2
Primeiramente, vamos retirar a fonte de tensão contínua e abrir o circuito, no ramo onde está a fonte de corrente.
Antes, bora passar os elementos pro domínio da frequência:
E o nosso circuito fica do seguinte jeito:
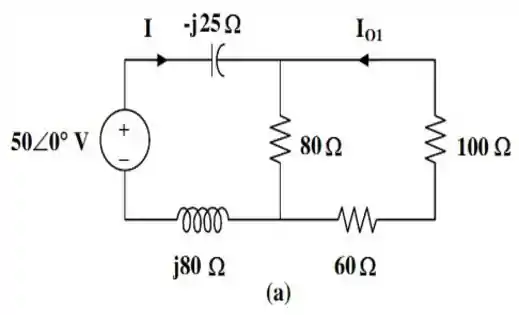
Os resistores de e estão em série. E o resultado dessa associação está em paralelo com a resistência de . De forma que a resistência equivalente para essa parte do circuito vale...
E a corrente vai ser dada pela divisão da fonte de tensão pela impedância total do circuito
Essa corrente vai se separar em duas outras correntes, quando chegar no nó superior do circuito. E por divisão de corrente, temos que a corrente nesse caso, vai ser dado por:
Passando pro domínio do tempo:
Passo 3
E por último, vamos deixar apenas a fonte de tensão contínua, exluindo a fonte de tensão alternada e abrindo o circuito no ramo onde está a fonte de corrente.
Nesse caso, como estamos trabalhando com tensão contínua, o indutor vira um curto circuito e o capacitor se torna um circuito aberto.
Desse modo, nosso circuito fica assim:
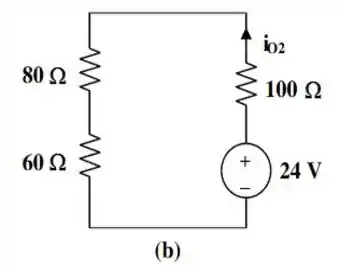
E a nossa corrente é dada facilmente, por:
Passo 4
Nesse último caso, vamos excluir a fonte de tensão contínua e a fonte de tensão alternada, deixando apenas a fonte de corrente.
Antes de pensar em como vai ficar o circuito, bora passar os elementos pro domínio da frequência:
Desse jeito, o nosso circuito vai ficar com a seguinte aparência:
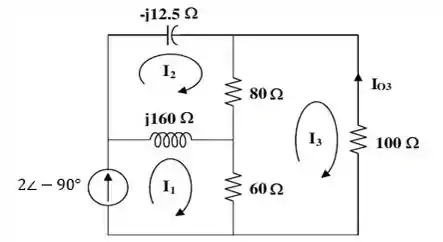
Vamos usar a lei das malhas para descobri o valor de .... Como podemos ver na figura acima, é o negativo da corrente de malha ...
Bom! Não precisa aplicar a para a malha ; afinal de contas podemos ver facilmente que:
Agora sim! Aplicando a para a malha :
E aplicando a para a malha :
Substituindo em :
Passando para polar
Desse modo, a corrente é dada por:
Passando para o domínio do tempo:
Passo 5
Por fim, temos apenas que somar as correntes obtidas para achar :